Plaques et Coques minces
La dynamique des plaques et des coques minces en régime de grande amplitude est étudiée (non-linéarité géométrique). Les modèles utilisés sont généralement issus des hypothèses de Von Karman (analogue dynamique de Von Karman pour les plaques, modèles de Donnell-Mushtari-Vlasov pour les coques). On s'intéresse particulièrement aux pertes de stabilité des solutions unimodales. Les relations de résonance interne sont alors cruciales pour expliquer les échanges d'énergie et les solutions couplées multimodales.
Plaques circulaires minces
La résonance 1:1, qui intervient pour les plaques circulaires pour tous les modes asymétriques, a été étudié théoriquement et expérimentalement. Ci-dessous, la courbe de résonance montrant le couplage entre les deux configurations.
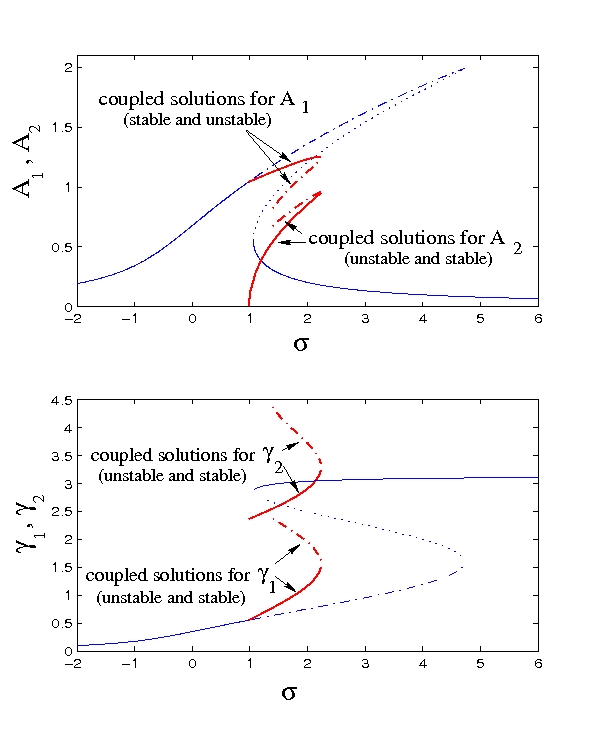
Articles liés
- C. Touzé, O.Thomas et A. Chaigne : Asymmetric non-linear forced vibrations of free-edge circular plates, part I: theory, Journal of Sound and Vibration, vol 258, No 4, pp. 649-676, 2002.
[ScienceDirect/JSV]
- O.Thomas, C. Touzé et A. Chaigne : Asymmetric non-linear forced vibrations of free-edge circular plates, part II: experiments, Journal of Sound and Vibration, vol 265, No 5, pp. 1075-1101, 2003.
[ScienceDirect/JSV]
Coques
Le cas des coques sphériques peu profondes a donné lieu à l'étude de la résonance 1:1:2. On montre ci-dessous les courbes de résonance théoriques et expérimentales pour ce cas particulier.
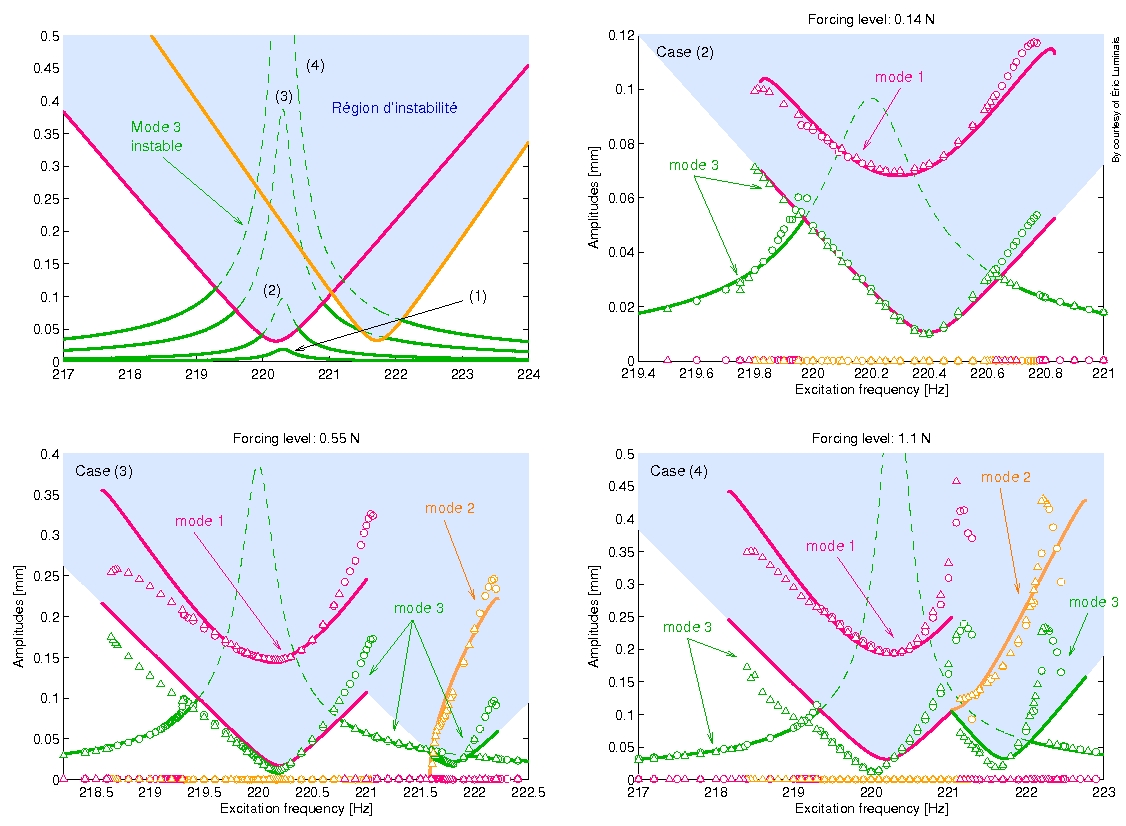L'étude de la tendance de non-linéarité, lorsque l'on augmente la courbure des coques sphériques, a pu être menée à bien grâce au formalisme des modes non-linéaires. Enfin des réductions de modèles ont été menées avec la technique des MNLs sur divers modèles de coques et panneaux à double courbure, avec des modèles plus raffinés que ceux de Donnell, en conservant l'inertie longitudinale. Le cas des coques cylindrique a donné lieu à une comparaison entre la méthode POD et la réduction par modes non-linéaires.
Articles liés
- O.Thomas, C. Touzé et A. Chaigne : Non-linear vibrations of free-edge thin spherical shells: modal interaction rules and 1:1:2 internal resonance, International Journal of Solids and Structures, vol. 42, No. 11-12, pp 3339-3373, 2005.
[ScienceDirect/IJSS]
- O.Thomas, C. Touzé et E. Luminais : Non-linear vibrations of free-edge thin spherical shells: experiments on a 1:1:2 internal resonance, Nonlinear Dynamics, vol. 49, No. 1-2, pp. 259-284, 2007.
[SpringerLink/NLDyn]
- C. Touzé et O.Thomas : Non-linear behaviour of free-edge shallow spherical shells: Effect of the geometry, International Journal of non-linear Mechanics, vol. 41, No. 5, pp. 678-692, 2006.
[ScienceDirect/IJNLM]
- M. Amabili et C. Touzé : Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic non-linear normal modes methods, Journal of Fluids and Structures, vol. 23, No. 6, pp. 885-903, 2007.
[ ScienceDirect/JFS]
- C. Touzé, M. Amabili et O. Thomas : Reduced-order models for large-amplitude vibrations of shells including in-plane inertia, Computer Methods in Applied Mechanics and Engineering, vol. 197, No. 21-24, pp. 2030-2045, 2008.
[ScienceDirect/CMAME]
Imperfections géométriques
Les imperfections géométriques (défauts de forme) pour les plaques circulaires et les coques minces, ont été étudiées dans le cadre de la thèse de Cédric Camier (soutenue le 2 Février 2009). La figure ci-dessous montre une déformée opérationnelle mesurée sur une coque de laboratoire pour le mode (0,2) (gauche), la déformée modale prédite par un modèle de coque parfaite (centre) et la correction apportée par un modèle de coque imparfaite prenant l'imperfection géométrique mesurée de la coque (de l'ordre de l'épaisseur h=1mm, droite).
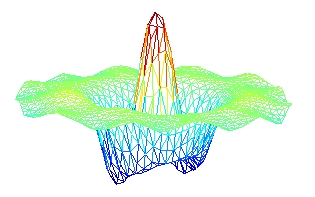
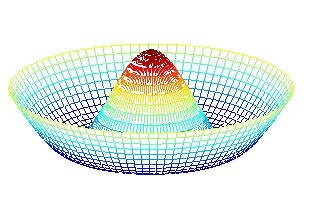
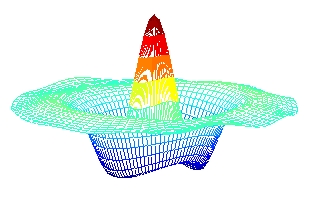
Articles liés
- C. Camier, C. Touzé et O. Thomas : Non-linear vibrations of imperfect free-edge circular plates and shells, Eur. J. Mechanics, A/solids, vol. 28(3), pp. 500-515, 2009.
[ScienceDirect/EJM-A]
- C. Touzé, C. Camier, G. Favraud et O. Thomas : Effect of imperfections and damping on the type of non-linearity of circular plates and shallow spherical shells, Mathematical problems in Engineering, vol. 2008, Article ID 678307, 19 pages, doi:10.1155/2008/678307, 2008.
[MPE | pdf]
Transition vers le chaos
La transition des solutions périodiques aux états chaotiques est étudiée pour les plaques circulaires minces, parfaites et imparfaites, à bord libre, dans le cadre des modèles utilisant les développements modaux utilisés pour étudier les premières bifurcations. Le but est de reproduire le schéma de transition vers le chaos observé génériquement pour les coques minces, cf. la page sur les gongs et les cymbales. Les EDPs sont donc projetées sur une base suffisamment riche de modes propres (de 20 à 30 modes sont utilisés dans les simulations), et les EDOs resultantes sont intégrées en temps en utilisant un schéma BDF pour les problèmes raides. Les résultats sont représentées en utilisant des sections de Poincaré (stroboscopie à la période du forçage externe). Ci-dessous, le cas d'une plaque imparfaite, montrant l'apparition d'un doublement de période avant l'instauration du régime chaotique.
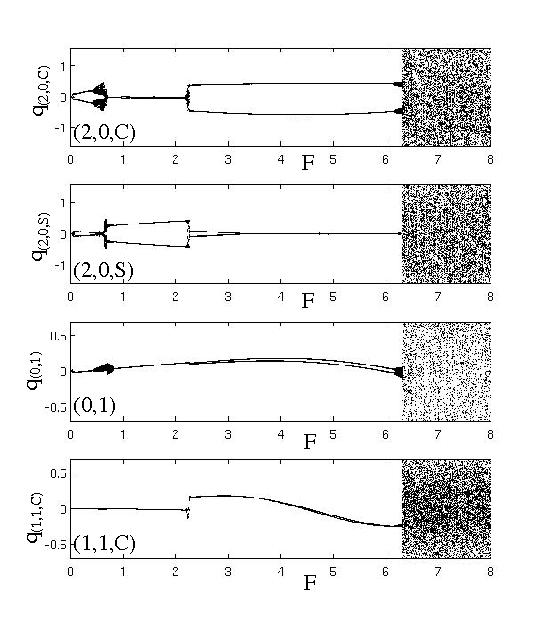
Articles liés
- C. Touzé, O. Thomas and M. Amabili : Forced vibrations of circular plates: from periodic to chaotic motions, ASME/IDETC 2010 (International Design Engineering Technical Conference), Montreal, Québec, Canada, 15-18 Aout 2010.
[ pdf ]
- C. Touzé, O. Thomas and M. Amabili : Transition to chaotic vibrations for harmonically forced perfect and imperfect circular plates, submitted to International Journal of Non-linear Mechanics, 2009.
