Modes non-linéaires en théorie des vibrations
Les modes normaux non-linéaires sont définis dans le cadre de la théorie des systèmes dynamiques comme des variétés invariantes de l'espace des phases, tangents à l'origine aux sous-espaces propres (modes linéaires) considérés. Cette définition donne un cadre adéquat pour la réduction de modèles : en projetant la dynamique sur ces sous-espaces invariants on obtient des modèles réduits prédisant les éléments essentiels (bifurcations) de la dynamique. Ci-dessous, le mode non-linéaire (variété invariante) pour un problème à deux degrés de liberté.
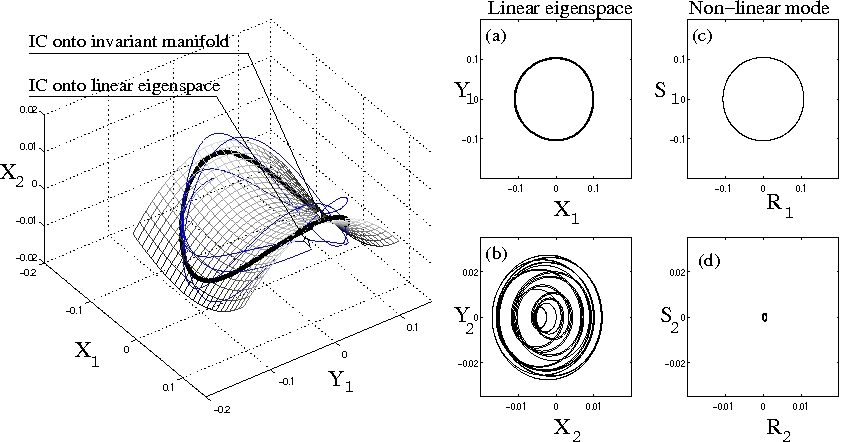Une méthode fondée sur théorie des formes normales a été développée afin de calculer asymptotiquement les modes non-linéaires. L'application de la méthode au cas des coques minces a permis entre autre de :
- Calculer la tendance de non-linéarité pour les coques spéhriques et les plaques imparfaites.
- Montrer des gains en temps de calcul d'un facteur 25 par rapport à l'utilisation de modes linéaires, en régime forcé harmonique.
- Comparer avec la méthode POD plus classiquement utilisée, montrant qu'à amplitude modérée les résultats étaient meilleurs.
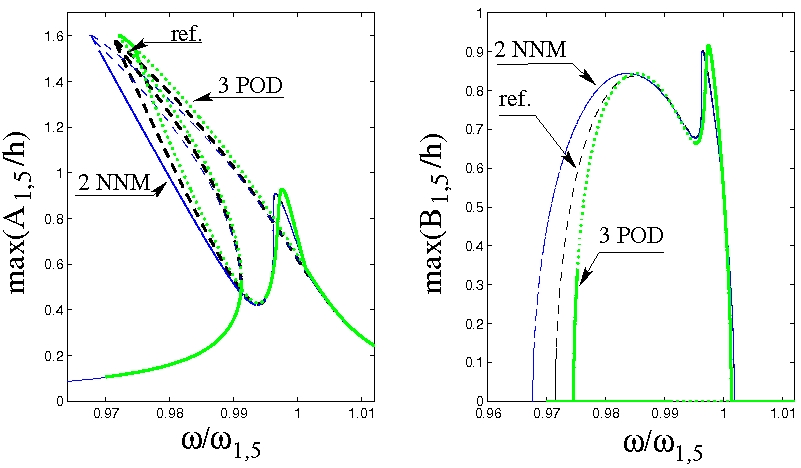
Ci-dessous : comparaison de la réponse en fréquence pour une coque cylindrique forcée harmoniquement au voisinage d'une résonance d'un mode compagnon, comparaison entre un solution de référence (noire), le modèle réduit obtenu avec 2 modes non-linéaires (bleu) et celui obtenu avec 3 modes POD (vert).
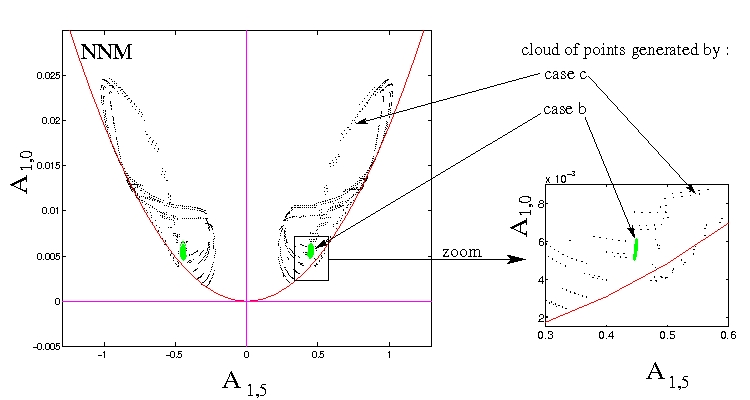
Section de Poincaré dans l'espace des phases, montrant la meilleure approximation --en terme de sous-espace-- donnée par le mode non-linéaire (MNL, ligne courbe proche des points de la simulation complète), comparée au sous-espace (linéaires) donnés par la méthode POD.
Documents
- Fascicule distribué lors de la journée nationale AFM/SFA
"Modes non-linéaires : Définitions et applications",
organisée le 18 Novembre 2005 au CNAM, comprenant une bibliographie sélective.
[document PDF]
- Présentation ("tutoriel") donnée à l'IRCAM lors de la journée d'étude SFA/GSAM "Non-linéarités et instruments de musique", le 21 janvier 2008.
[document PDF]
Notes de cours CISM
- C. Touzé : Normal form theory and nonlinear normal modes: Theoretical settings and applications, lecture notes et chapitre de livre, cours du CISM "Modal Analysis of nonlinear mechanical systems", Udine, Italie, 25-29 Juin 2012.
[document PDF]
Articles liés
- C. Touzé, O.Thomas et A. Chaigne : Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes, Journal of Sound and Vibration, vol 273, No 1-2, pp 77-101, 2004.
[ScienceDirect/JSV]
- C. Touzé et O.Thomas : Non-linear behaviour of free-edge shallow spherical shells: Effect of the geometry, International Journal of non-linear Mechanics, vol. 41, No. 5, pp. 678-692, 2006.
[ScienceDirect/IJNLM]
- C. Touzé et M. Amabili : Non-linear normal modes for damped geometrically non-linear systems: application to reduced-order modeling of harmonically forced structures, Journal of Sound and Vibration, vol. 298, No. 4-5, pp. 958-981, 2006.
[ScienceDirect/JSV]
- M. Amabili et C. Touzé : Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic non-linear normal modes methods, Journal of Fluids and Structures, vol. 23, No. 6, pp. 885-903, 2007.
[ ScienceDirect/JFS]
- C. Touzé, M. Amabili et O. Thomas : Reduced-order models for large-amplitude vibrations of shells including in-plane inertia, Computer Methods in Applied Mechanics and Engineering, vol. 197, No. 21-24, pp. 2030-2045, 2008.
[ScienceDirect/CMAME]
