Plates and shells
Non-linear dynamics of thin plates and shells with large-amplitude motions (geometrical non-linearity), is studied. The Von Karman stress-strain relationship is used, giving rise to the so-called analog dynamic of Von karman model for plates, and Donnell-Mushtari-Vlasov models for shells. A particular emphasis is put on the loss of stability of unimodal solutions. Internal resonance relationships are curcial in order to explain energy exchange and appearance of multimodal solutions.
Cicular plates
Due to the rotational symmetry, 1:1 resonances exist for every asymmetric mode. The coupling creating by this internal resonance has been studied theoretically and experimentally. Below is shown a frequency-reponse curve in the vicinity of the 1:1 resonance, showing the coupling between the two configurations.
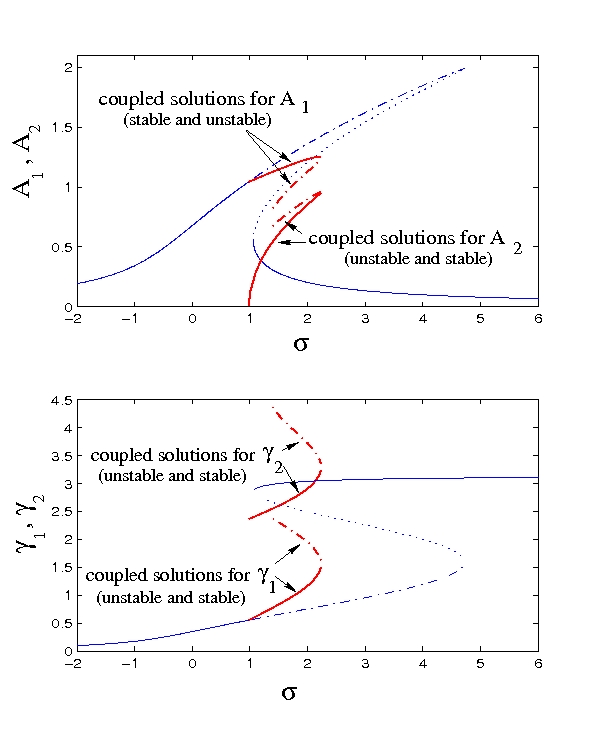
Related articles
- C. Touzé, O.Thomas et A. Chaigne : Asymmetric non-linear forced vibrations of free-edge circular plates, part I: theory, Journal of Sound and Vibration, vol 258, No 4, pp. 649-676, 2002.
[ScienceDirect/JSV]
- O.Thomas, C. Touzé et A. Chaigne : Asymmetric non-linear forced vibrations of free-edge circular plates, part II: experiments, Journal of Sound and Vibration, vol 265, No 5, pp. 1075-1101, 2003.
[ScienceDirect/JSV]
Shells
The case of a shallow psherical shell has been studied both theoretically and experimentally. The particular case of a 1:1:2 internal resonance has been investigated and experimentally demonstrated, see the frequency-reponse curves below.
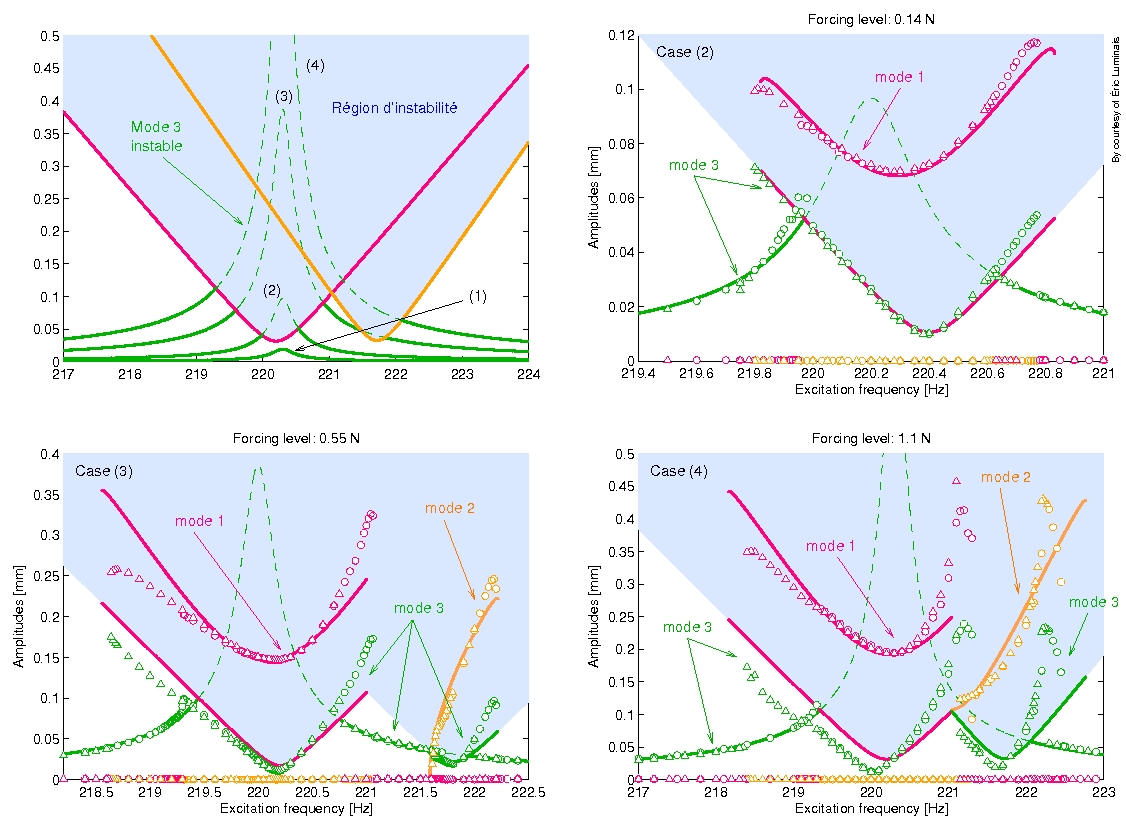The type of non-linearity (hardening or softening behaviour) has been studied thanks to the NNMs formalism. Lastly, reduced-order models has been built for different panels and doubly-curved shells, with refined stress-strain relationship obtained by including in-plane inertia. Finally the case of circular cylindrical shell has been used to compare NNM reduction method to the Proper Orthogonal Decomposition (POD).
Related articles
- O.Thomas, C. Touzé et A. Chaigne : Non-linear vibrations of free-edge thin spherical shells: modal interaction rules and 1:1:2 internal resonance, International Journal of Solids and Structures, vol. 42, No. 11-12, pp 3339-3373, 2005.
[ScienceDirect/IJSS]
- O.Thomas, C. Touzé et E. Luminais : Non-linear vibrations of free-edge thin spherical shells: experiments on a 1:1:2 internal resonance, Nonlinear Dynamics, vol. 49, No. 1-2, pp. 259-284, 2007.
[SpringerLink/NLDyn]
- C. Touzé et O.Thomas : Non-linear behaviour of free-edge shallow spherical shells: Effect of the geometry, International Journal of non-linear Mechanics, vol. 41, No. 5, pp. 678-692, 2006.
[ScienceDirect/IJNLM]
- M. Amabili et C. Touzé : Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic non-linear normal modes methods, Journal of Fluids and Structures, vol. 23, No. 6, pp. 885-903, 2007.
[ ScienceDirect/JFS]
- C. Touzé, M. Amabili et O. Thomas : Reduced-order models for large-amplitude vibrations of shells including in-plane inertia, Computer Methods in Applied Mechanics and Engineering, vol. 197, No. 21-24, pp. 2030-2045, 2008.
[ScienceDirect/CMAME]
Geometric imperfections
Geometric imperfections for circular plates and thin shells, have been studied in the framework of the PhD thesis of Cédric Camier (defended on February 2, 2009). Below is shown an operating deflection shape experimentally measured on a shallow shell in the lab (left), for mode (0,2). It is compared to the prediction given by a perfect shell model, center. The geometric imperfections are in this case of the order of the thickness (1 mm), they have been measured and inserted into an imperfect shell model, predicting the mode shape shown right.
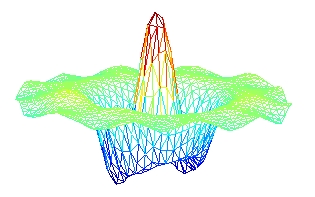
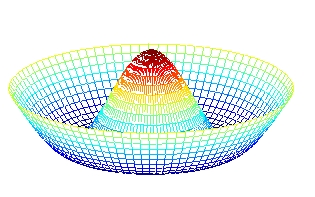
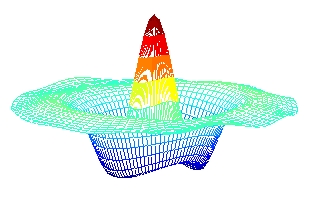
Articles liés
- C. Camier, C. Touzé et O. Thomas : Non-linear vibrations of imperfect free-edge circular plates and shells, Eur. J. Mechanics, A/solids, vol. 28(3), pp. 500-515, 2009.
[ScienceDirect/EJM-A]
- C. Touzé, C. Camier, G. Favraud et O. Thomas : Effect of imperfections and damping on the type of non-linearity of circular plates and shallow spherical shells, Mathematical problems in Engineering, vol. 2008, Article ID 678307, 19 pages, doi:10.1155/2008/678307, 2008.
[MPE | pdf]
Transition to chaos
The transition from periodic to chaotic vibrations is studied for thin circular plates with a free edge, in the framework of the models used to study the first transition, ie by using a modal procedure for discretizing the PDEs of motion. The ail is to reproduce numerically the transition scenario that is generically observed for thin shells, see the page on gongs and cymbals. A Gear's BDF procedure is used for integrating the resultants equations of motion in time, taht is needed to face the numerical stiffness of the problem. results are presented with Poincaré's stroboscopic cross-section. Below, the case of an imperfect plate showing a period-doubling before the onset of chaos.
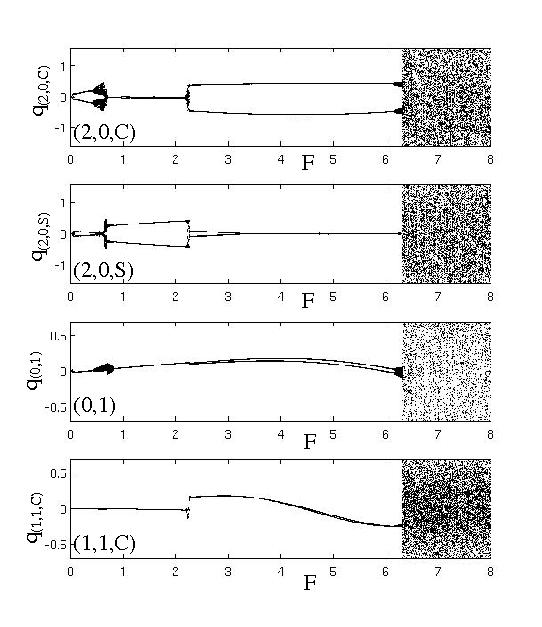
Articles liés
- C. Touzé, O. Thomas and M. Amabili : Forced vibrations of circular plates: from periodic to chaotic motions, ASME/IDETC 2010 (International Design Engineering Technical Conference), Montreal, Québec, Canada, 15-18 Aout 2010.
[ pdf ]
- C. Touzé, O. Thomas and M. Amabili : Transition to chaotic vibrations for harmonically forced perfect and imperfect circular plates, submitted to International Journal of Non-linear Mechanics, 2009.
