Non-linear Normal Modes (NNMs) in vibration theory
Non-linear Normal Modes (NNMs) are defined in the framework of dynamical systems theory, as invariant manifolds in phase space, tangent at origin to their associated eigenspaces (linear modes). This definition provides an adequate tool for model reduction :
projecting the dynamics on these invariant manifolds, performant reduced-order models are obtained taht are qualitatively accurate in the sense that they predict the correct type of non-linearity, as well as the correct local bifurcation diagram. Below is represented the first NNM for a two-degree-of-freedom system.
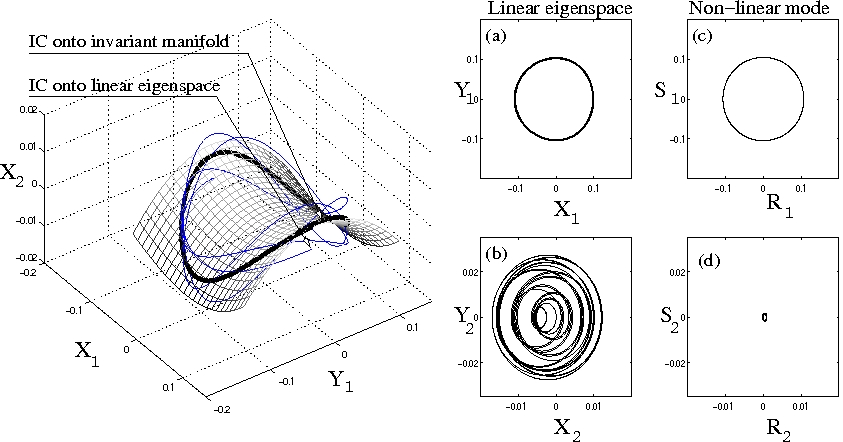A method based on real normal form theory has been developped in order to provide an asymptotic computation of the NNMs. The method has been applied to numerous continuous models for thin shells, showing, amongst other things:
- The method allows a parametric prediction of the type of non-linearity, it has been applied in the case of a shallow spherical shells, as well as for imperfect plates.
- In the case of an external harmonic forcing, simulation times has been divided by a factor 25, as compared to traditional method based on a Rayleigh-Ritz approach with, as for a functional basis, the linear normal modes.
- Comparison with the more classical POD method has shown that a better reduction is obtained for moderate non-linearity. Computational time is also saved in the construction of the reduced model.
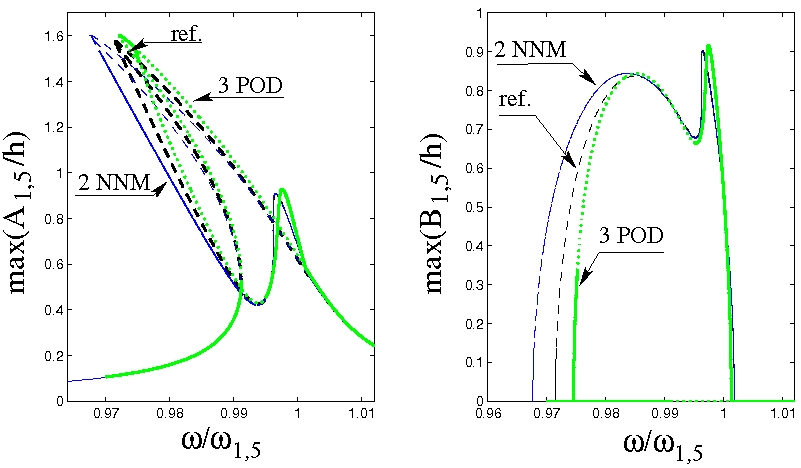
Below : Comparison of frequency-response curves for a water-filled circular cylindrical shell that is excited in the vicinity of an asymmetric mode. Reference solution, in black, has been obtained with 16 linear modes, it is compared to the NNM solution (2 dofs, blue) and to the POD solution (3 dofs, green).
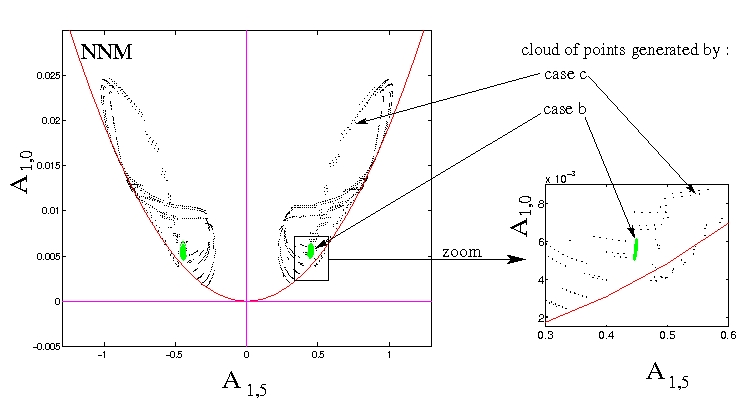
Poincaré cut in phase space corresponding to the preceding case, showing the better approximation provided by the invariant manifold (NNM, curved line very close to the reference simulation points) compared to the linear spaces given by the POD method.
Lecture notes at CISM
- C. Touzé : Normal form theory and nonlinear normal modes: Theoretical settings and applications, lecture notes and book chapter, CISM symposium "Modal Analysis of nonlinear mechanical systems", Udine, Italy, 25-29 Juin 2012.
[document PDF]
Related articles
- C. Touzé, O.Thomas et A. Chaigne : Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes, Journal of Sound and Vibration, vol 273, No 1-2, pp 77-101, 2004.
[ScienceDirect/JSV]
- C. Touzé et O.Thomas : Non-linear behaviour of free-edge shallow spherical shells: Effect of the geometry, International Journal of non-linear Mechanics, vol. 41, No. 5, pp. 678-692, 2006.
[ScienceDirect/IJNLM]
- C. Touzé et M. Amabili : Non-linear normal modes for damped geometrically non-linear systems: application to reduced-order modeling of harmonically forced structures, Journal of Sound and Vibration, vol. 298, No. 4-5, pp. 958-981, 2006.
[ScienceDirect/JSV]
- M. Amabili et C. Touzé : Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic non-linear normal modes methods, Journal of Fluids and Structures, vol. 23, No. 6, pp. 885-903, 2007.
[ ScienceDirect/JFS]
- C. Touzé, M. Amabili et O. Thomas : Reduced-order models for large-amplitude vibrations of shells including in-plane inertia, Computer Methods in Applied Mechanics and Engineering, vol. 197, No. 21-24, pp. 2030-2045, 2008.
[ScienceDirect/CMAME]
