L'instabilité d'orbite radiale

Alors que les deux instabilité fondamentales de Jeans (détails) et d'Antonov (détails), responsables respectivement de l'effondrement global et du cœur, conduisent généralement à une forme sphérique , l'instabilité d'orbite radiale permet de s'en écarter.
Apparue dès le début des années soixantes dans les travaux d'Antonov, puis reprise dans une série d'article conclue par nos travaux analytiques ou numériques, l'instabilité d'orbite radiale se produit pour des systèmes caractérisés par un équilibre dont la dispersion de vitesse est fortement radiale. Ce type de système est réceptif à toutes les perturbations non radiales (voir ci-dessous). Une direction privilégiée (arbitraire, issue de fluctuations) se manifeste donc et le système se s'allonge selon un axe.

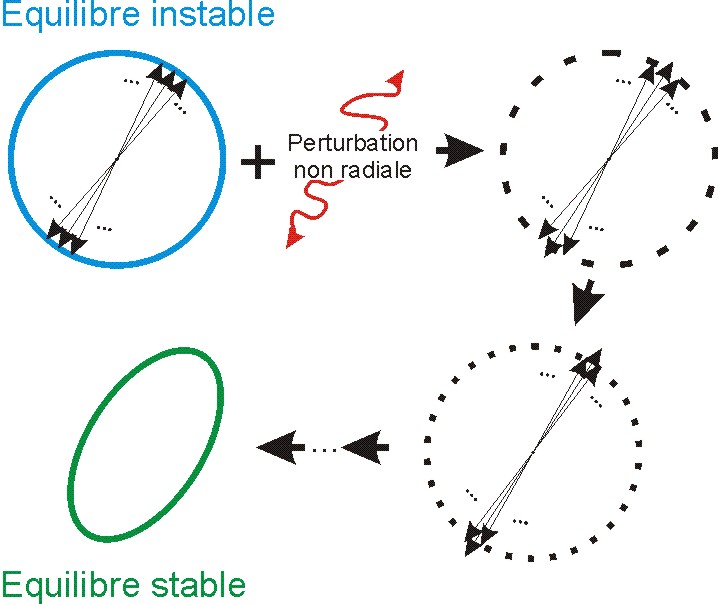
Pour un système d'Ossipkov-Merrit (détails) avec un rayon d'anisotropie radiale r_a=2, nous avons pu réaliser le film ci-dessous qui montre bien l'apparition de l'instabilité sur une échelle de quelques temps dynamiques.

Différentes analyses (détails) semblent montrer que cette instabilité pourrait bien être à l'origine de la forme d'un partie des galaxies elliptiques : L'effondrement d'un halo de points répartis de façon homogène sur un système auto-gravitant à l'équilibre (un modèle de Plummer) développe une instabilité d'orbite radiale ou non suivant que l'effondrement est violent (beaucoup d'énergie cinétique radiale est transmise) ou non (peu d'énergie cinétique radiale est transmise). On obtient un effondrement violent ou calme en jouant sur le rapport du viriel initial du halo. (quelques films très illustratifs)

Toutes les simulations on été réalisées au Pole de Calcul Parallèle de l'ENSTA.