Le fameux modèle de Plummer

Pour plus de détails sur les grandeurs ou les calculs ci-dessous il est bon de se référer au cours de gravitation. Si vous trouvez des erreurs n'hésitez pas à me les signaler...

Le modèle de Plummer est une solution stationaire sphérique entièrement analytique du système de Vlasov-Poisson. Il constitue un modèle acceptable pour représenter certains amas globulaires.

La fonction de distribution d'un modèle de Plummer est de type polytropique :

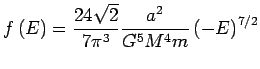Le paramètre réel 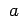est libre, l'énergie est celle d'une particule test de masse liée au système dont la masse totale est . On obtient la densité de masse d'un tel système en intégrant la fonction distribution sur l'espace des vitesses. On trouve :

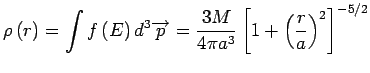Le modèle de Plummer est donc non borné dans l'espace des positions, mais sa masse est finie. Le potentiel gravitationnel associé à cette distribution de masse est la solution de l'équation de Poisson 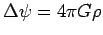, on trouve :

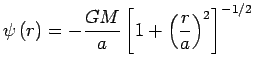Le caractère polytropique de ce système se manifeste par la relation 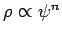avec 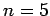dans le cas du modèle de Plummer.

En plus de ces fonctions principales, on peut calculer analytiquement la plupart des grandeurs physiques pour un tel modèle :

• La masse contenue dans un rayon 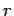donné :

• La dispersion de vitesse à la distance :

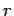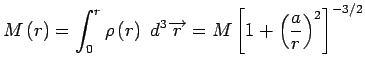
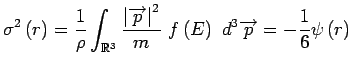
Le modèle de Plummer est isotrope dans l'espace des vitesses, comme tous les systèmes dont la fonction de distribution ne dépend que de l'énergie...
L'énergie potentielle gravitationnelle totale contenue dans un modèle de Plummer se calcule aussi complètement :

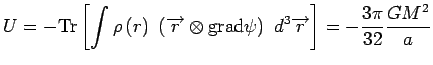Le modèle de Plummer est une solution stationnaire du système de Vlasov-Poisson, il est donc à l'équilibre du viriel (voir exemple). L' énergie cinétique totale contenue dans un tel système est donc :

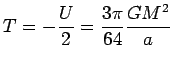On peut même calculer le rayon de la sphère contenant 50% de la masse totale :

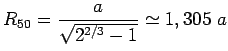Et son temps dynamique que l'on obtient par exemple comme :

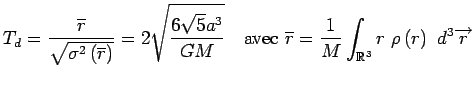Ces modèles, lorsqu'ils sont isolés, sont connus pour être stable contre à peu près toutes les perturbations, linéaires ou non...