The isochrone potentials theory


The theory of isochrone potentials was initiated by Michel Hénon in
1958.
We developed it significantly in 2018 in the paper SPD.
We propose to give here the flavour of this paper without the details.
Generalities
A particle of mass $m$ with position $\vec{r}$ in orbit in the radial potential$\psi \left( r\right) $ got a conserved energy $E=m\xi $ and angular momentum $\vec{L}=m\vec{\Lambda }$. The motion takes place in the plane which is orthogonal to $\vec{\Lambda }$ and the radial distance $r$ fulfills the ODE \begin{equation} \frac{1}{2}\left( \frac{dr}{dt}\right) ^{2}=\xi -\frac{\Lambda ^{2}}{2r^{2}}-\psi \left( r\right)\;\;\;\left[1\right] \end{equation} If the orbit is bounded and non radial (i.e. don't pass throught the origin) the solution of this equation is periodic: $\exists \tau <\infty $, $r\left( t+\tau \right) =r\left( t\right) $. This period depends generically on both the parameters of the equation, i.e. $\tau=\tau \left( \xi ,\Lambda \right) $.
Two classical examples of isochrones potential are existing:
- The harmonic (or Hooke) potential $\psi _{\mathrm{ha}}\left( r\right) =\frac{1}{2}\omega ^{2}r^{2}$, with $\omega \in \mathbb{R}^{+}$ in which all the non radial bounded orbits are ellipses and share the same period $\tau =2\pi /\omega $ which depends neither on the energy nor on the angular momentum.
- The Kepler potential $\psi _{\mathrm{ke}}\left( r\right) =-\mu /r$ with $\mu \in \mathbb{R}^{+}$ in which all the non radial bounded orbits are ellipses with a semi-major axis $a=\mu /\left( 2\left\vert \xi \right\vert \right)$ which one focus at the center of the system. In such a potential the third Kepler law indicates that $2\tau^{2}\left\vert \xi \right\vert ^{3}=\pi ^{2}\mu ^{2}$. The period is then independant from $\Lambda $.

The globular cluster 47 Toucan (NGC104) - Distance : 15 KAl - Size : 140 Al
Let's observe the mass repartition in a globular cluster. On the first hand
we remark that the center is homogeneous (constant density) and then well described by a harmonic potential, and on the other hand, that particles which are confined in the
surrounds of the cluster feel it as a point with the total mass $M$ of the system, the later are then in a Kepler potential with $\mu =GM$.
In the late of fiveties, Michel Hénon has the idea to join both the internal and external regions by looking for a new isochrone potential under the whole system.
Parabolas at the heart of isochrony
In his seminal paper , Michel Hénon introduces a clever change of variables: the radial distance $r$ and the potential $\psi$ are replaced by some news, that we will call Hénon's ones, which are $x=2r^2 $ and $Y(x) = x\psi(x)$. The ODE $[1]$ then writes:
The use of these new variables reveals the isochrone property.
Radial oscilations $r(t)$ take place between two extremal values: the nearest distance from the center, called periastron $(r_{p} \leftrightarrow x_{p})$, and
the greatest distance from the center, called apoastron $(r_{a} \leftrightarrow x_{a})$.
These extremal distances are obtained when $\displaystyle\frac{dr}{dt}=0$ which is when $\displaystyle\frac{dx}{dt}$ vanishes too. Inspecting $[2]$ one can see that this later condition
correspond to the intersections between the staight line $y=\xi x- \Lambda ^{2}$ and the graph of the function $Y(x)$ in the $xy$ plane.
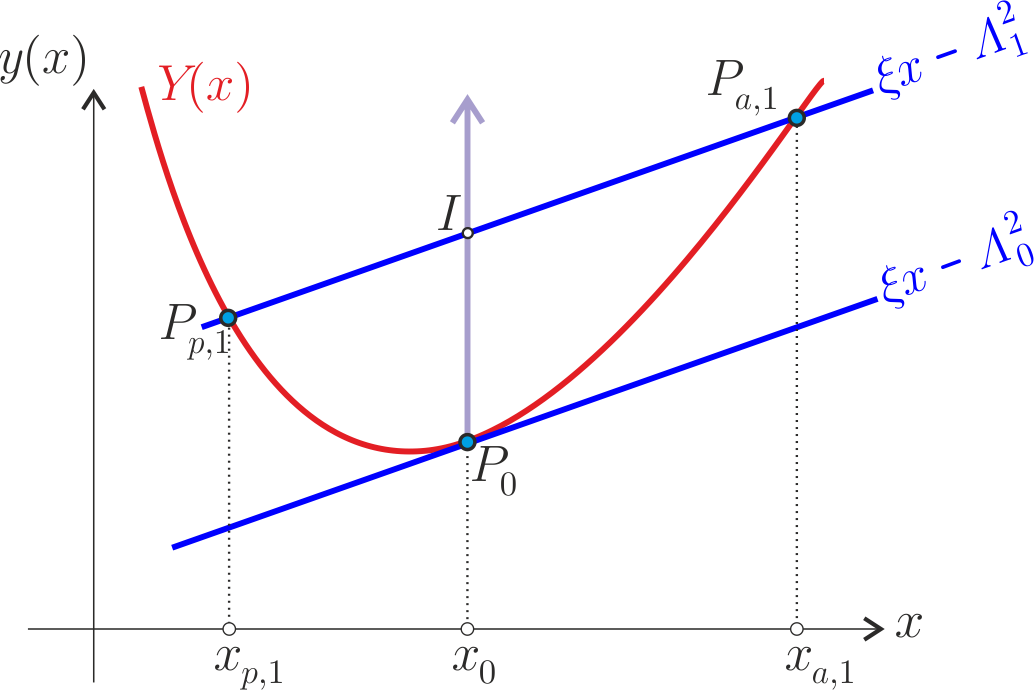
An orbit is included in the curve $Y(x)$ between the two extremal values. On the above figure, we have represented two orbits sharing the same energy $\xi$ but with different values of the angular momentum: $\Lambda _{0}$ (circular orbit) and $\Lambda _{1}$. On this figure, the isochrone property occurs when the distance $P_{0} I$ is proportional to the square of the chord $P_{p,1} P_{a,1}$. This property characterise also a parabola.
The complete proof of this theorem is given in the appendix B of SPD.
It is also proven that this parabola must have a piece of its graph in the $x\geq 0$ plane for physical relevance (because $x=2 r^2 $).
Hence, parabolas of interest are the ones with 1 or 2 intersections with the $Oy$ axis.
Finally, one can show that a bounded orbit in a increasing gravitationnal isochrone potential is included in a convex arc of parabola.
It exists only four kinds of isochrone potentials
The fundamental equation $\left[2\right]$ depends on both the two parameters $\xi$ and $\Lambda$.
- Adding a constant $\epsilon$ to the energy, $\xi\to \xi+\epsilon$, can be absorbed by the transformation $Y(x)\to Y(x) -\epsilon x$ and let the ODE $\left[2\right]$ globaly invariant. In the $xy$ plane, it is equivalent to apply \[ \left( \begin{array}{c}x^\prime \\ y^\prime \end{array}\right) = \left[ \begin{array}{cc} 1 & 0 \\ \epsilon & 1 \end{array} \right] \left( \begin{array}{c}x\\y\end{array} \right)\; . \] This transformation is a transvection. It swivells a straight line of slope $a$ into another one of slope $a+\epsilon$ keeping the same intersections with the $0y$ axis. It transforms a parabola into a parabola which intersections (1 or 2) with the $Oy$ axis are the same and the symetry axis is swivelled by a additive slope $\epsilon$. The vertical tangent of this parabola is keeping the same abscissa.
- Adding a constant $\lambda^2$ to the angular momentum can be absorbed by the transformation $Y(x)\to Y(x) -\lambda^2$ to remain unchanged the fundamental ODE. In the $xy$ plane, it is equivalent to apply a vertical translation to the whole parabola.
It exists only 4 kinds of distinct isochrone parabolas under the combined action of a transvection and a translation. This can be viewed graphically (or more preciselly here SPD...) observing the action of transvection under parabolas in the movies below:
| Left | Right | Laid | Staight |
Each of this kind of parabola is represented by its element which possess a horizontal or vertical tangent exactly at the origin. The action of the group $\mathbb{A}$ of $\epsilon-$transvections and $\lambda-$translations under these four elements generates the whole set of isochrone parabolas. The set of corresponding isochrone potentials can then be extracted from them.
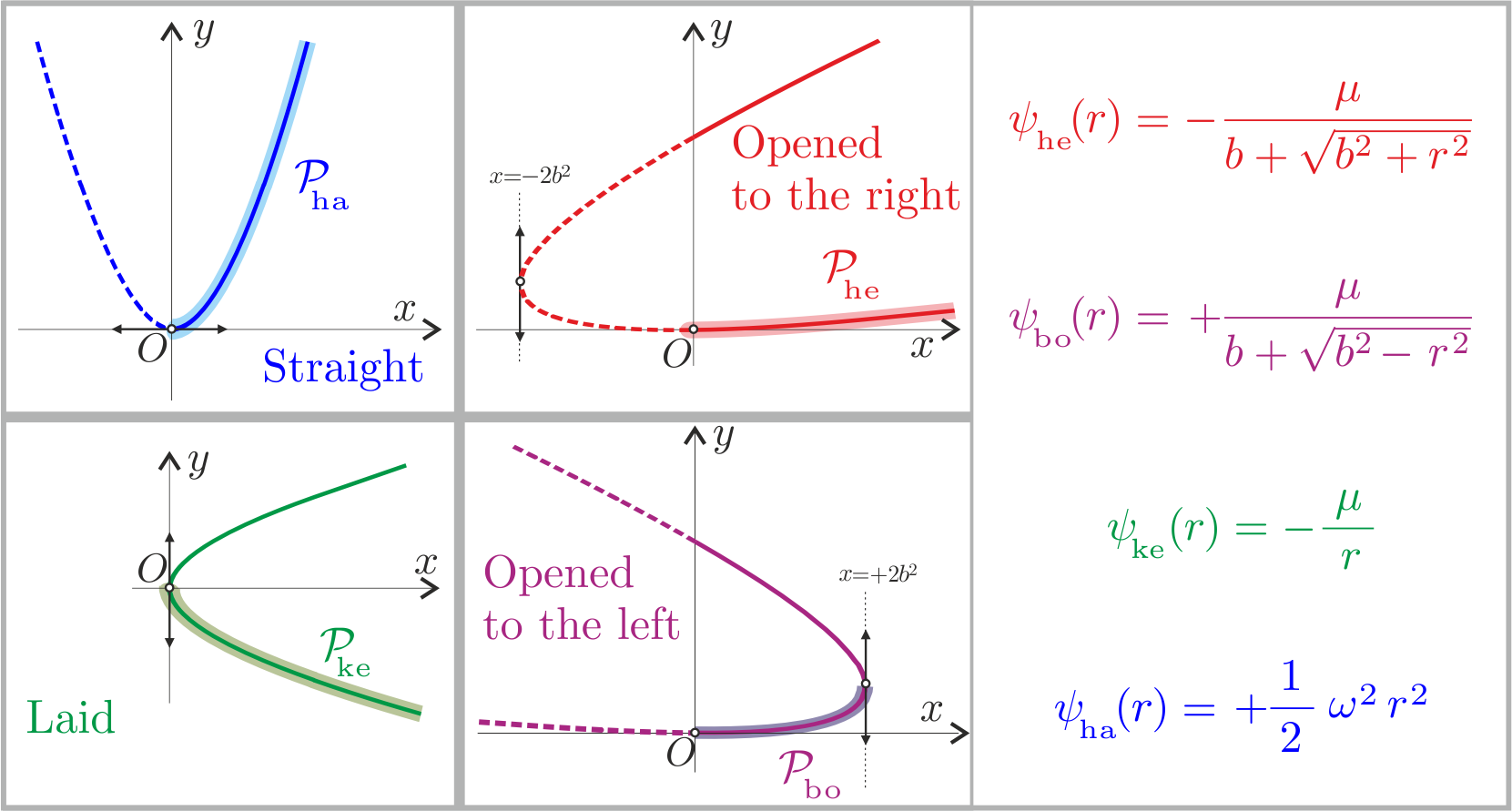
Physically, the transvection just adds the constant $\epsilon$ to the potential, this changes only the origin of potentials. On the other side, translations add a
gauge $j(r)=\frac{\lambda^2}{2 r^2}$ to the potential: it modifies its physical properties preserving its isochrone character.
The main difference between the four elements presented in the figure consists in the distribution of their mass. It is a point mass for the Kepler
while it is uniformly distributed in the harmonic. As expected, the mass of the Hénon is a continuous mix between a uniform core and diffuse halo, finally the bounded has an increasing mass distribution !
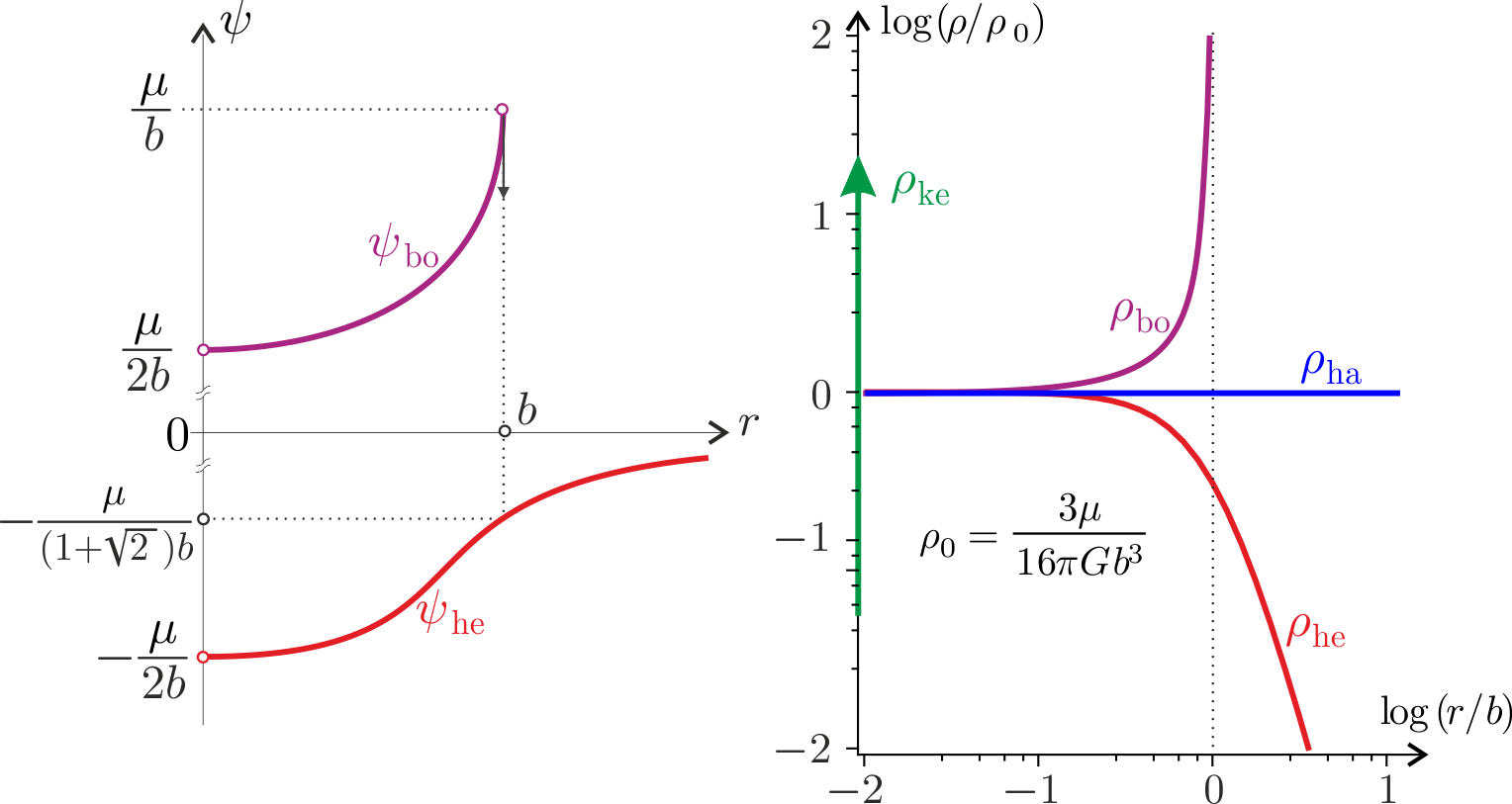
Hénon and bounded potentials on the left and mass density of isochrones on the right.
The theory of isochrone relativity
The action of the sub-group $\mathbb{A}$ of the plane affinities cannot allow to send a keplerian orbit to another kind of isochrone one.
Nevertheless, it is well known from (Bohlin, 1911 or Levi-Civita, 1906) that such a mapping is possible in some special cases:
These transformations maps a keplerian orbit into a harmonic one and vice-versa by exchanging totaly the role of the energy $\xi$ and the potential $\psi$.
We have generalized these tranformations by introducing a partial exange of both these physical quantities.
This exchange must be linear in order to preserve the parabolic nature of the graph of $x\mapsto Y(x)$.
Introducing the affine coordinates $w=(\xi x, y)$ we name Bolst this transformation, it writes
\[
\left( \begin{array}{c}\xi^\prime x^\prime \\
y^\prime
\end{array}
\right)
=
\underbrace{
\left[ \begin{array}{cc} \alpha & \beta \\
\alpha - 1 & \beta +1
\end{array}
\right]
}_{B_{\alpha,\beta}}
\left( \begin{array}{c}\xi x\\y\end{array} \right)
\;\;\;\alpha \in \mathbb{R}, \;\beta \in \mathbb{R},\; \alpha+\beta\ne 0.
\]
One can restrict Bolts to their symmetric form without loss of generality. It then depends on the only parameter $\gamma=\alpha+\beta$.
These $\boldsymbol{i}-$Bolst (for symmetr$\boldsymbol{i}$c Bolts) has an action which is very similar to a change of reference frame in special relativity
(see here).
The later are commonly called Boosts, it justifies the name we give for our isochrone transformations which are generalizing Bohlin ones.
On the figure below we have represented the $B_{\gamma}$ action under the canonical frame $\mathcal{R}=(O,i,j)$.
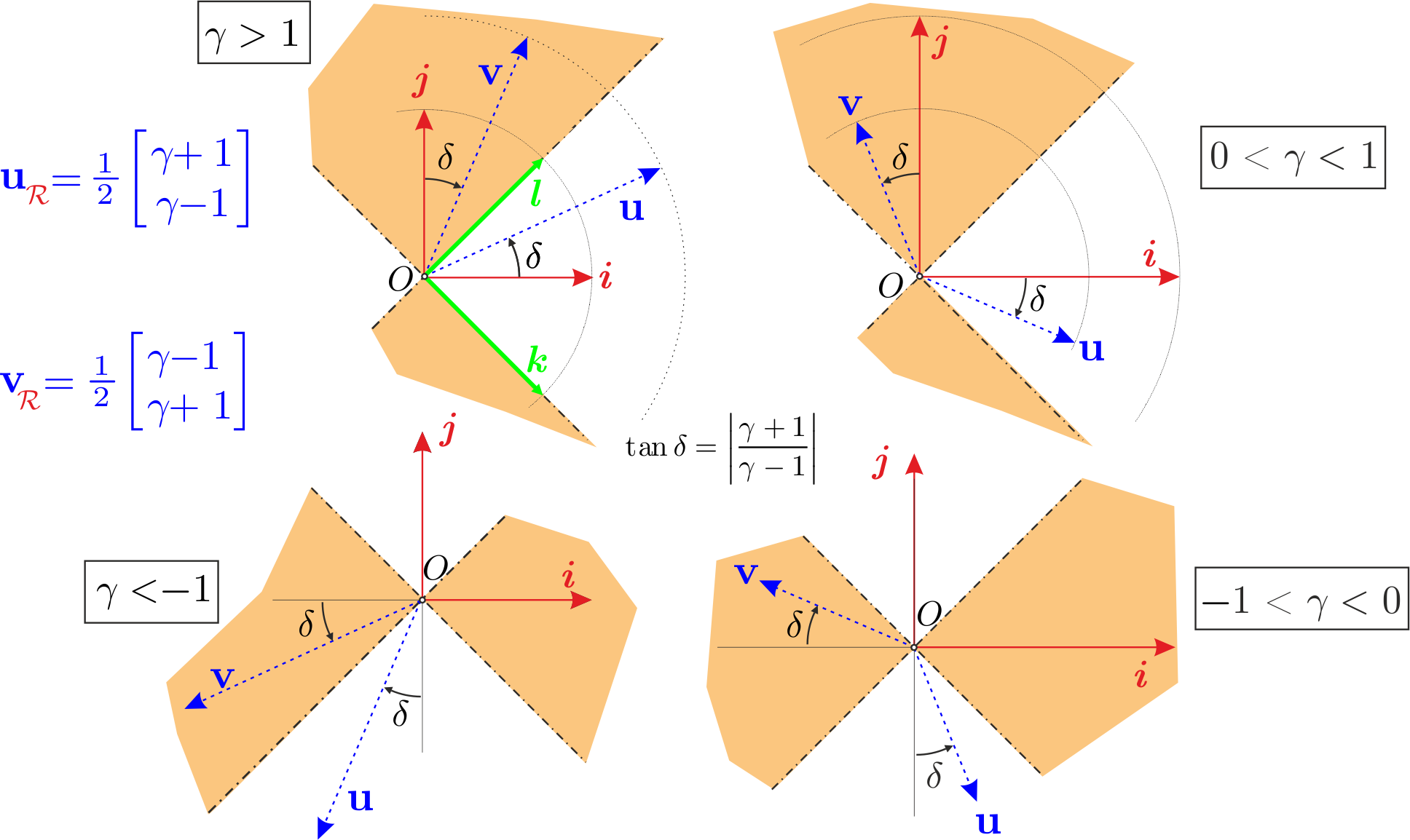
The bolsted frame $\mathcal{R}^\prime=(O,\mathbf{u},\mathbf{v})$ image of $\mathcal{R}$ by $B_{\gamma}$ is the combined result of a hyperbolic rotation and a homothety.
The eigenvectors $\boldsymbol{l}$ and $\boldsymbol{k}$ of $B_{\gamma}$ define a cone which is globally invariant under an $\boldsymbol{i}-$Bolst.
A proper frame can be associated to each isochrone parabola $\mathcal{P}$. It is the frame defined by the two units vectors generating respectively
the symmetry axis $\mathcal{S}(\mathcal{P})$ of the parabola and its tangent at the origin $\mathcal{T}_O (\mathcal{P})$.
A trivial remark consists in viewing that the proper frame of the keplerian parabola is the canonical one $\mathcal{R}$.
On the movie below one can see the action of a $\gamma >1$ $\boldsymbol{i}-$Bolst under this canonical keplerian parabola.
As soon as the $\boldsymbol{i}-$Bolst starts, the blue bolsted parabola has two intersections with $Oy$ red canonical axis, in addition it is right oriented:
it is then a Hénon parabola. However it remains keplerian (with only one intersection with the ordinate axis) in its proper black frame. This is the theory of isochrone relativity.
In the figure below, we show how to transfer any parabola to a keplerian one using only transvections,
translations and $\boldsymbol{i}-$Bolst which engendrate together the Bolst group.
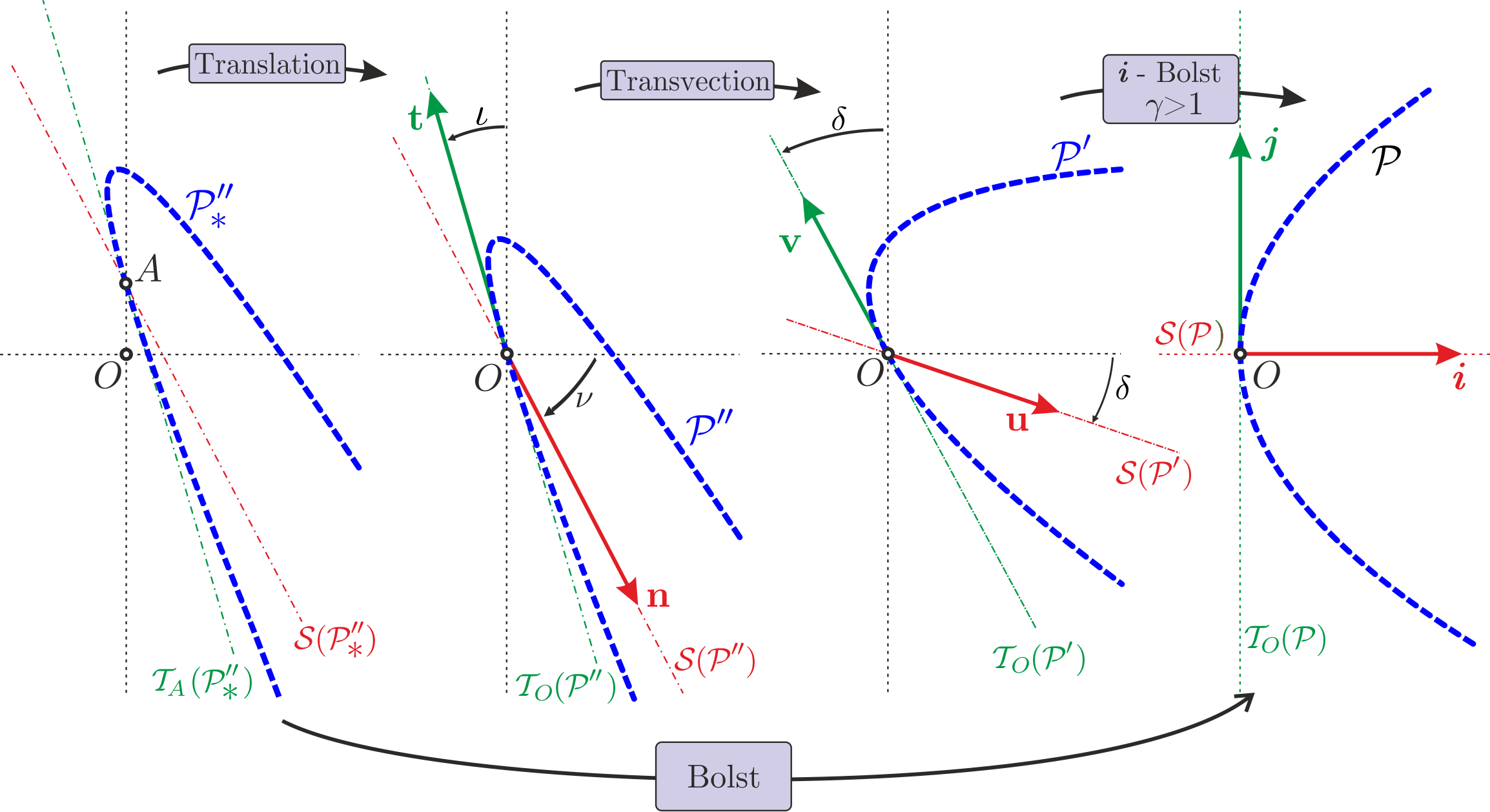
It can be shown that an orbit is isochrone if and only if it is the image of a keplerian orbit by a Bolst:
To be or not to be isochrone depends on the fact that you are keplerian in your proper frame!
As in special relativity, in isochrony there are conserved intervals, a proper time, a same writing of the physical equations in all frames, invariant cones containing vectors
sharing the same properties...
In order to conclude these illustrations, we let you think about this video which showing in the same panel parabolas, motions in the $(x,y)$ plane and the corresponding orbits
in the usual polar coordinates.
Some isochrone facts
The generalisation of Kepler's laws
The isochrone relativity allows us too show that an isochrone orbit is keplerian in its own frame.
But we know from Kepler that such an orbit has a special property: The cube of its semi-major axis is proportionnal to the square of its period.
Each isochrone orbit in its potential has an apoastron $r_a$, a periastron $r_p$, an energy $\xi$ and an angular momentum $\Lambda$.
This periodic orbit has a period $\tau$ and on each period its periastron moves by an angle $\Delta \varphi = 2\pi n_p$. These orbital parameters are gathered in the following table:

The third Kepler law holds for all isochrones !
Bertrand's Theorem
In 1873, Joseph Bertrand showed that in 3D, the only potential for which all non radial bounded orbits ar closed are the keplerian and the harmonice ones.
Since the end of the nineteen century a lot of proofs were given and this subject stayed still alive until now to find the best proof of this important feature
(see here).
In the land of isochrony, this theorem becomes a simple corrolary...
As a matter of fact, it is well known that the period and the periastron motion are partial derivatives of the radial action:
\[
\mathcal{A}_r=\frac{1}{\pi}\int_{r_p}^{r_a}\sqrt{2\left[\xi-\psi(r)\right]-\frac{\Lambda^2}{r^2}}dr
\;\;\Longrightarrow\;\;
\left\{
\begin{array}{ccc}
\tau &=& 2\pi \displaystyle\frac{\partial \mathcal{A}_r}{\partial \xi} \\
& & \\
n_p &=& - \displaystyle\frac{\partial \mathcal{A}_r}{\partial \Lambda} \\
\end{array}
\right.
\]
For the orbit to be closed we must have $n_p\in 2\pi\mathbb{Q}$.
Under this hypothesis the function $(\xi,\Lambda)\mapsto n_p$ is continuous from $\mathbb{R}^2\to 2\pi\mathbb{Q}$.
Then it is a constant function as the set $\mathbb{R}\setminus\mathbb{Q}$
is dense in the set $\mathbb{R}$.
A direct use of Schwarz's Theorem then gives\[
\frac{\partial n_p}{\partial \xi} =0
\;\;\Longrightarrow\;\;
\frac{\partial^2 \mathcal{A}_r}{\partial \xi\partial \Lambda} =0
\;\;\Longrightarrow\;\;
\frac{\partial \tau}{\partial \Lambda} =0
\]
To fullfills of the Bertrand's Theorem conditions it is thus necessary that the considered potential be isochrone.
By inspecting the possible values of $n_p$, we see clearly that only the keplerian and the harmonic possess all their non radial bounded orbit closed.
Isochrony as an initial state for some self-gravitating systems
In a recent study, we have shown numerically that the formation process of some self-gravitating systems (e.g. globular clusters or Lox Surface Brightness galaxies)
leads to an isochrone system well described by the Hénon potential.
So the circle comes back around!
Michel Hénon was wright in 1958,
Nethertheless several dynamical process, occuring over much longer time, as two body relaxation, tidal effects, etc. contribute to leave the isochronal initial state.
It is why observational data from these objects don't reaveal this character.
For more complex self-gravitating systems like High Surface Brightness galaxies, the hierarchical formation process erases since the begining the isochrone state and reveals
in fine a lot of properties that are to be understood.