La théorie des potentiels isochrones


La théorie des potentiels isochrones a été initiée par Michel Hénon en
1958.
Nous l'avons considérablement développée en 2018 dans l'article SPD.
Nous proposons d'en faire un petit résumé ci-dessous sans entrer dans tous les détails que vous trouverez dans notre article
SPD.
Généralités
Une particule de masse $m$ repérée par le vecteur $\vec{r}$ en orbite dans un potentiel gravitationnel radial $\psi \left( r\right) $ voit son énergie $E=m\xi $ et son moment cinétique $\vec{L}=m\vec{\Lambda }$ conservés. Le mouvement s'effectue dans le plan orthogonal à $\vec{\Lambda }$ et la distance radiale vérifie l'équation différentielle \begin{equation} \frac{1}{2}\left( \frac{dr}{dt}\right) ^{2}=\xi -\frac{\Lambda ^{2}}{2r^{2}}-\psi \left( r\right)\;\;\;\left[1\right] \end{equation} Si l'orbite est bornée et non radiale (i.e. ne passe pas par $r=0$) la solution de cette équation est périodique : $\exists \tau <\infty $, $r\left( t+\tau \right) =r\left( t\right) $. Cette période dépend généralement des deux paramètres de l'équation, i.e. $\tau=\tau \left( \xi ,\Lambda \right) $.
Il existe deux exemples classiques de potentiels isochrones :
- Le potentiel harmonique $\psi _{\mathrm{ha}}\left( r\right) =\frac{1}{2}\omega ^{2}r^{2}$, avec $\omega \in \mathbb{R}^{+}$ dans lequel toutes les orbites bornées non radiales sont des ellipses et possèdent la même période $\tau =2\pi /\omega $ qui ne dépend ni de l'énergie ni du moment cinétique de la particule considérée;
- Le potentiel keplerien $\psi _{\mathrm{ke}}\left( r\right) =-\mu /r$ avec $\mu \in \mathbb{R}^{+}$ dans lequel toutes les orbites bornées non radiales sont des ellipses de demi grand-axe $a=\mu /\left( 2\left\vert \xi \right\vert \right) \ $dont l'un des foyers est le centre du système et pour laquelle la 3$^{\mathrm{\grave{e}me}}$ loi de Kepler indique que $2\tau^{2}\left\vert \xi \right\vert ^{3}=\pi ^{2}\mu ^{2}$. La période de chaque orbite ne dépend pas de $\Lambda $.

L'amas globulaire 47 Toucan (NGC104) Distance : 15 KAl -- Taille : 140 Al
Lorque l'on observe la répartition de la masse d'un amas globulaire, on
remarque d'une part que le centre est homogène (densité constante)
et donc associé à un potentiel harmonique et d'autre part que les
particules confinées dans les régions externes de l'amas le voient
comme un point de masse $M$, ces dernières ressentent donc un potentiel
keplerien avec $\mu =GM$.
En 1958, Michel Hénon propose de faire le lien entre les régions
centrales et les régions externes en cherchant un potentiel isochrone
à l'échelle de tout le système.
Les paraboles au cœur de la propriété isochrone
Dans son article original, Michel Hénon propose un changement de variable très astucieux : il remplace respectivement la distance radiale $r$ et le potentiel $\psi$ par les variables, dites de Hénon, $x=2r^2 $ et $Y(x) = x\psi(x)$. L'équation différentielle $[1]$ s'écrit alors :
Dans ces variables la propriété d'isochronie devient très élégante.
Les oscillations radiales $r(t)$ s'effectuent entre deux valeurs extrèmes : la distance la plus proche appelée périastre $(r_{p} \leftrightarrow x_{p})$, la distance la plus proche
éloignée appelée apoastre $(r_{a} \leftrightarrow x_{a})$.
Ces valeurs extrèmes sont atteintes lorsque $\displaystyle\frac{dr}{dt}=0$ ce qui correspond également aux points où $\displaystyle\frac{dx}{dt}$ s'annule soit, en observant $[2]$, les intersections
entre la droite $y=\xi x- \Lambda ^{2}$ et le graphe de la fonction $Y(x)$ dans le plan $xy$.
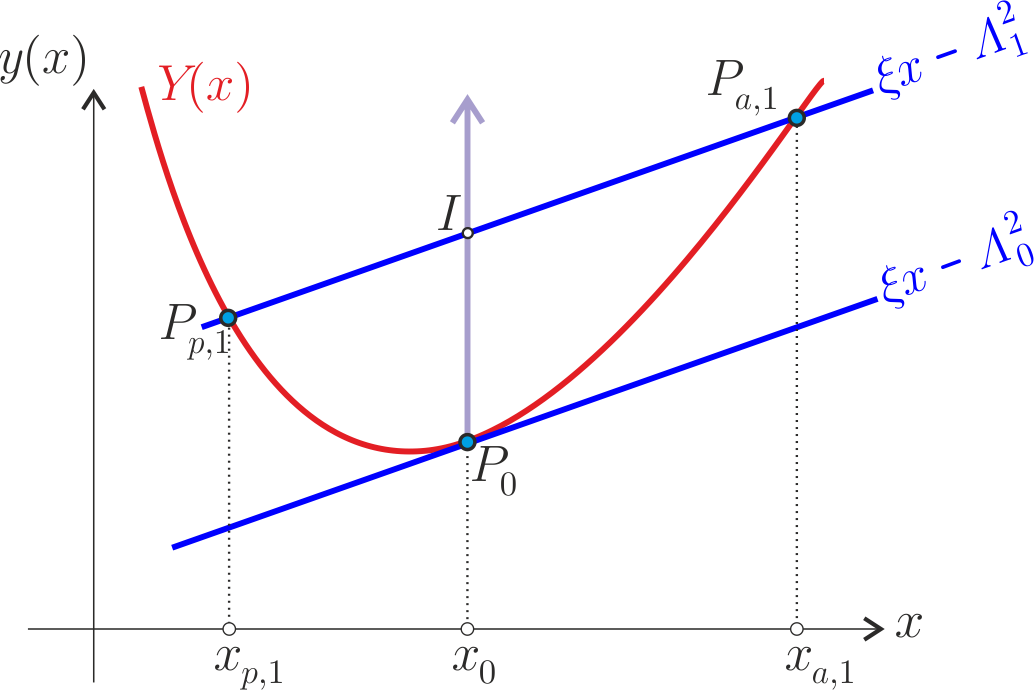
Une orbite s'effectue le long de la courbe $Y(x)$ entre les deux valeurs extrèmes. Sur la figure ci-dessus on a représenté deux orbites de même énergie $\xi$ mais avec différentes valeurs du moment cinétique : $\Lambda _{0}$ (orbite circulaire) et $\Lambda _{1}$. La propriété isochrone se caractérise sur cette figure par le fait que la hauteur $P_{0} I$ doit être proportionnelle au carré de la corde $P_{p,1} P_{a,1}$. Cette propriété caractérise également une parabole.
Une preuve complète de ce théorème se trouve dans l'appendice B de SPD.
On y montre également que cette parabole doit avoir au moins un morceau dans le plan $x\geq 0$ pour pouvoir être utilisée physiquement (car $x=2 r^2 $).
Les paraboles qui nous intéressent sont donc celle qui possèdent 1 ou 2 intersections avec l'axe $Oy$.
Une trajectoire bornée dans un potentiel gravitationnel (donc croissant) est incluse dans un arc convexe de parabole.
Il existe 4 types de potentiels isochrones
L'équation fondamentale $\left[2\right]$ dépend des deux paramètres $\xi$ et $\Lambda$.
- Si l'on ajoute une constante $\epsilon$ à l'énergie, $\xi\to \xi+\epsilon$, on peut l'absorber en effectuant la transformation $Y(x)\to Y(x) -\epsilon x$ et laisser ainsi l'équation $\left[2\right]$ globalement invariante. Dans le plan $xy$ cela revient à appliquer \[ \left( \begin{array}{c}x^\prime \\ y^\prime \end{array}\right) = \left[ \begin{array}{cc} 1 & 0 \\ \epsilon & 1 \end{array} \right] \left( \begin{array}{c}x\\y\end{array} \right)\; . \] Cette transformation est une transvection . Elle incline une droite de pente $a$ en une droite de pente $a+\epsilon$ en conservant la même intersection avec l'axe $0y$. Elle transforme une parabole en une parabole dont le ou les points d'intersections avec l'axe $0y$ sont invariants et l'axe de symétrie est incliné de $\epsilon$. La tangente verticale de cette parabole ne change pas d'abcsisse.
- Si l'on ajoute une constante $\lambda^2$ au moment cinétique, $\Lambda^2 \to \Lambda^2+\lambda^2$, on peut l'absorber en effectuant la transformation $Y(x)\to Y(x) -\lambda^2$ et laisser ainsi l'équation $\left[2\right]$ globalement invariante. Dans le plan $xy$ cela revient à appliquer uniquement une translation verticale à la parabole.
Il existe 4 familles de paraboles différentes sous l'action combinée d'une transvection et d'une translation, on peut s'en convaincre graphiquement (ou de façon plus précise : SPD...) en observant l'action des transvections ci-dessous.
| Gauche | Droite | Couchée | Dressée |
On représente chacune de ses familles par son élément qui possède sa tangente horizontale ou verticale exactement en l'origine. L'action du groupe $\mathbb{A}$ des $\epsilon-$transvections et des $\lambda-$translations sur ces quatre représentants fondamentaux engendre l'ensemble des paraboles isochrones. On peut en extraire les potentiels isochrones réduits associés.
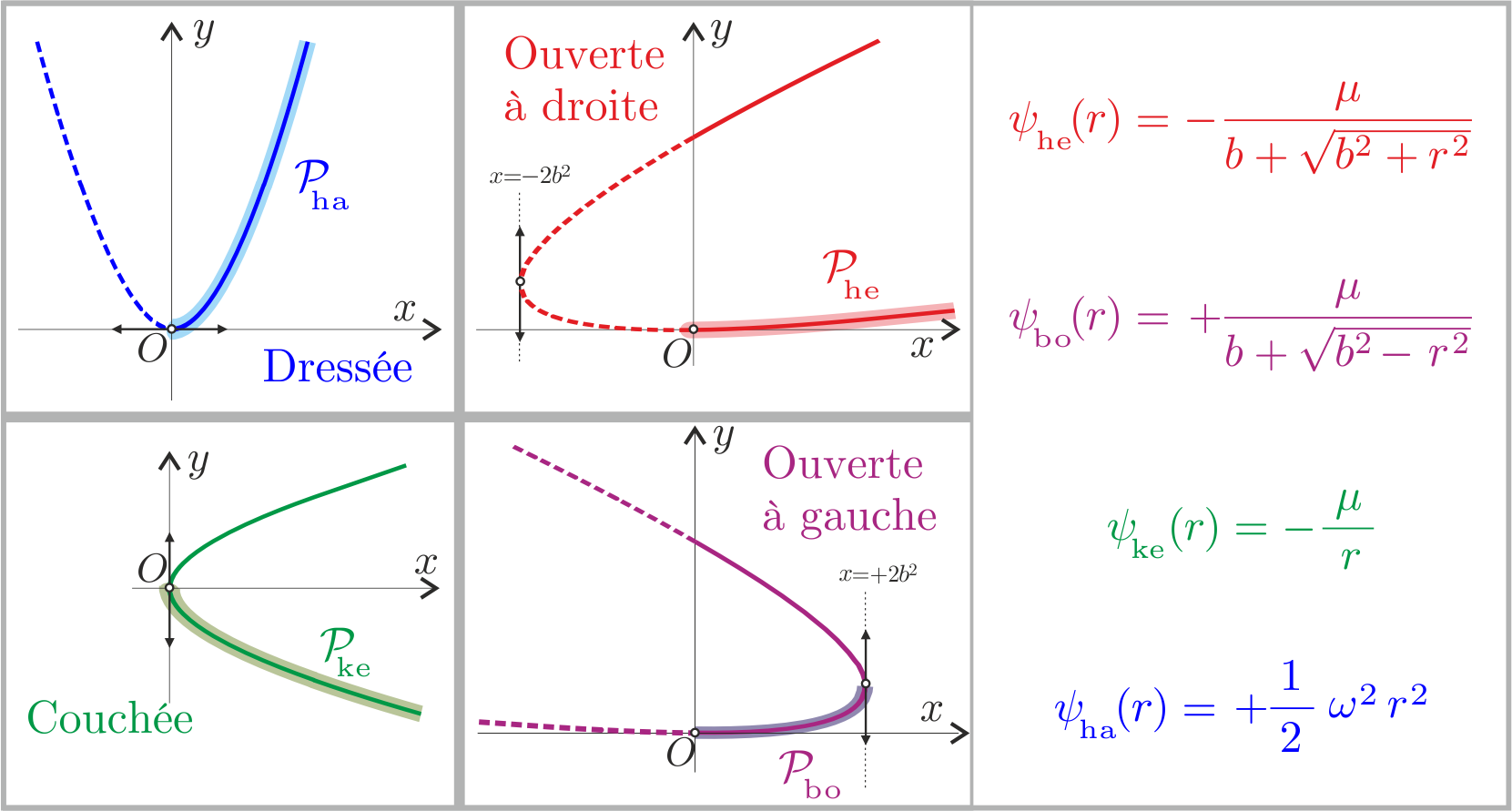
Physiquement la transvection ajoute une constante $\epsilon$ au potentiel ce qui change simplement l'origine de l'énergie potentielle. Par contre les translations ajoutent
une jauge $j(r)=\frac{\lambda^2}{2 r^2}$ au potentiel qui modifie ses propriétés physiques en préservant son caractère isochrone.
La différence fondamentale entre les 4 isochrones réduits consiste en la façon dont la masse est répartie à l'interieur de chacun : Elle est concentrée en un point dans le keplerien ou
uniformément répartie dans le domaine de définition de l'harmonique. Elle est répartie dans une structure en cœur-halo pour le Hénon et croit vers l'extéreur dans le borné.
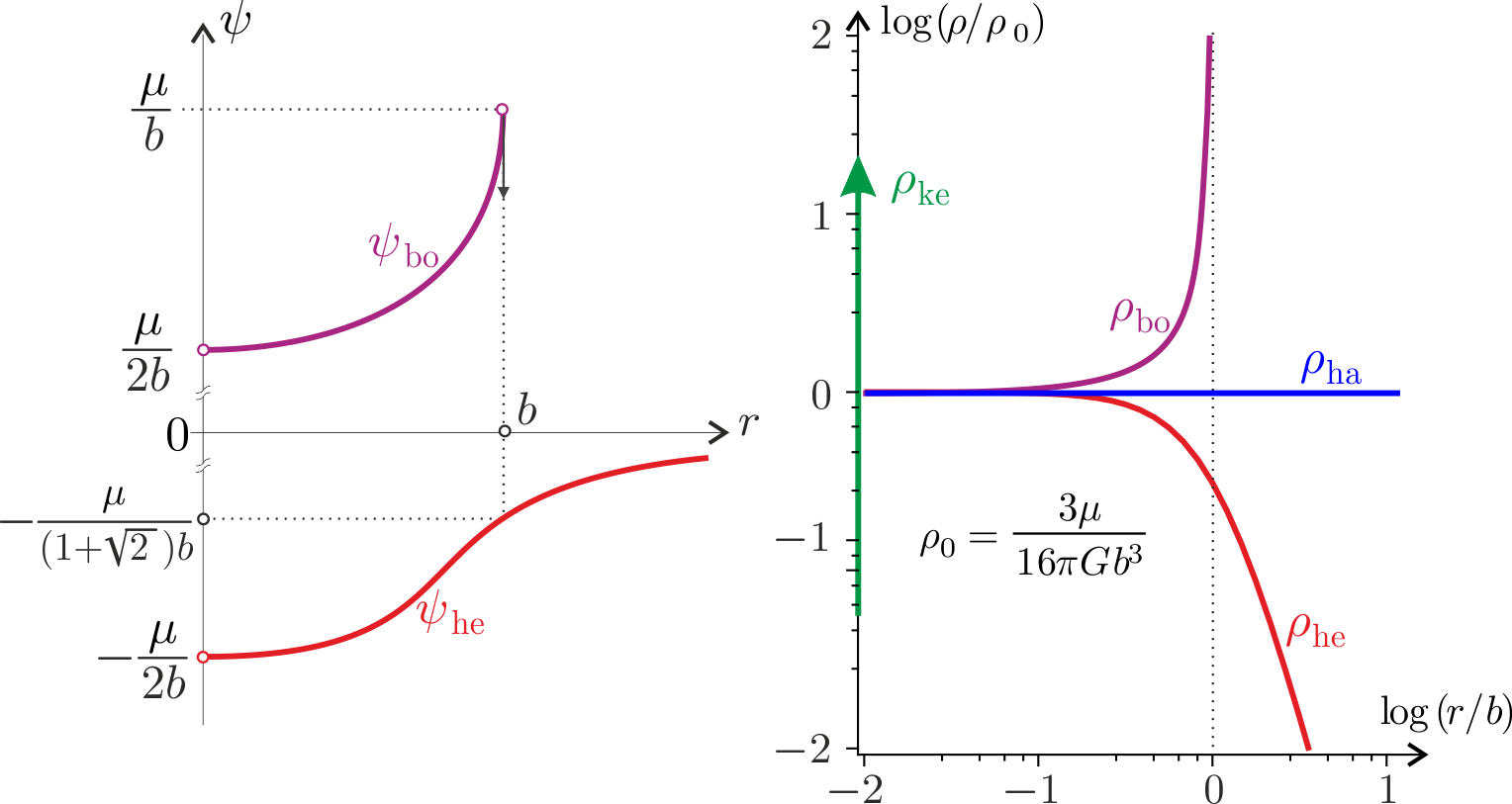
Les potentiels de Hénon et bornés et la densité volumique de masse des isochrones réduits (à droite)
La théorie de la relativité isochrone
L'action du sous-groupe $\mathbb{A}$ des affinités du plan ne permet pas d'envoyer une orbite keplerienne vers une orbite isochrone d'un autre type.
On savait pourtant qu'une telle transformation canonique est possible (Bohlin, 1911 ou Levi-Civita, 1906) : ces transformations transfèrent un mouvement keplerien
vers un mouvement harmonique et vice-versa en échangeant complètement le rôle de l'énergie $\xi$ et du potentiel $\psi$. Nous avons généralisé ces transformations
en introduisant un échange partiel de ces deux quantités. Cet échange doit être le résultat d'une transformation linéaire fin de préserver le caractère parabolique
du graphe de $x\mapsto Y(x)$.
En introduisant des coordonnées affines $w=(\xi x, y)$ cette transformation que nous avons appelé un Bolst, s'écrit
\[
\left( \begin{array}{c}\xi^\prime x^\prime \\
y^\prime
\end{array}
\right)
=
\underbrace{
\left[ \begin{array}{cc} \alpha & \beta \\
\alpha - 1 & \beta +1
\end{array}
\right]
}_{B_{\alpha,\beta}}
\left( \begin{array}{c}\xi x\\y\end{array} \right)
\;\;\;\alpha \in \mathbb{R}, \;\beta \in \mathbb{R},\; \alpha+\beta\ne 0.
\]
On peut restreindre les Bolts à leur version symétrique ne dépendant que du seul paramètre $\gamma=\alpha+\beta$. Ces $\boldsymbol{i}-$Bolst ont une action
tout à fait comparable aux changements de référentiel en relativité restreinte (voir ici).
Ces dernières sont parfois appelées des Boosts, ce qui justifie le nom que nous avons choisi pour nos transformations isochrones qui généralisent la transformation de Bohlin
et s'interprètent comme des changements de référentiel, le préfixe $\boldsymbol{i}$ précise le cas symétrique.
On a représenté sur la figure ci-dessous l'action de $B_{\gamma}$ sur le référentiel canonique $\mathcal{R}=(O,i,j)$ du plan.
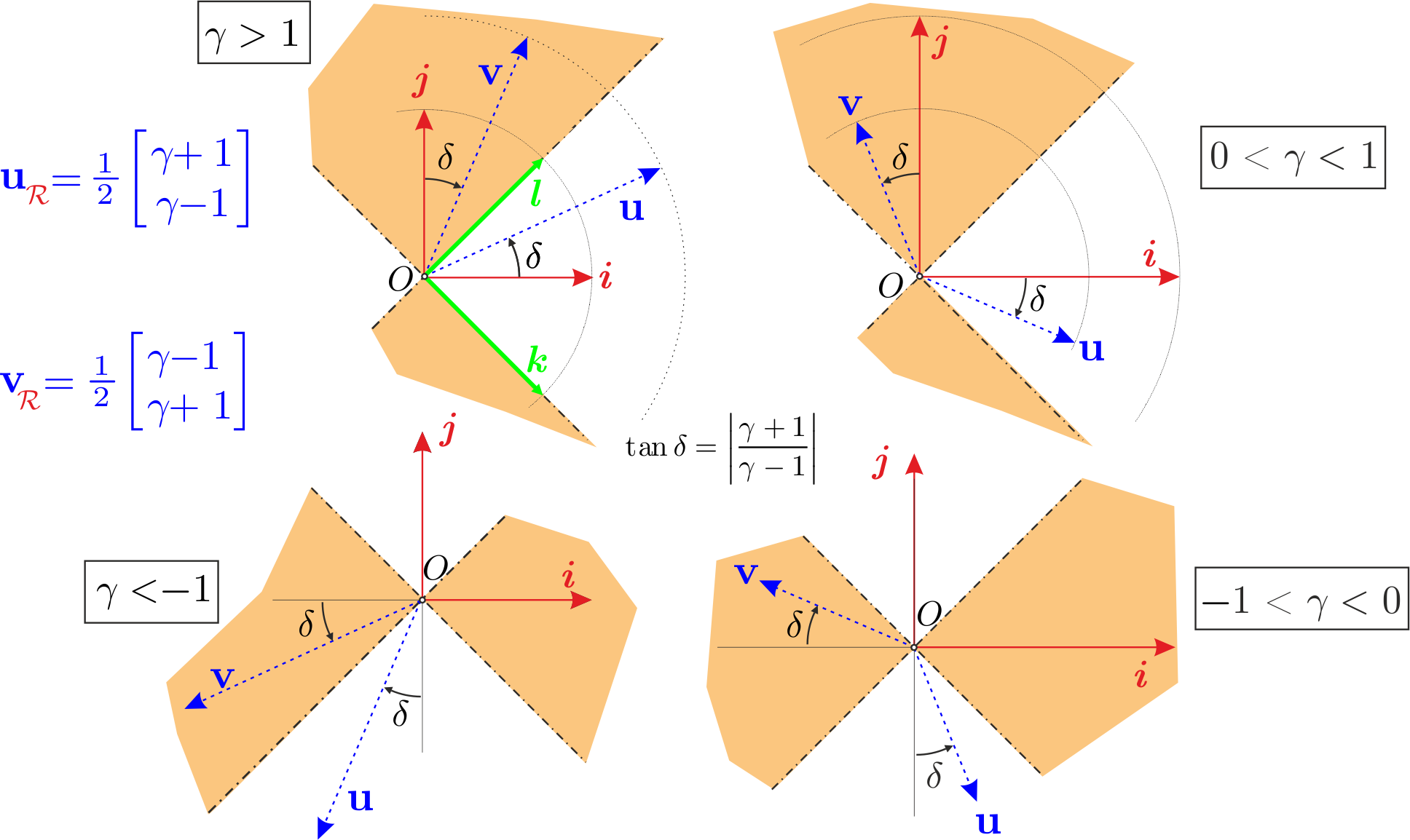
Le référentiel image $\mathcal{R}^\prime=(O,\mathbf{u},\mathbf{v})$ de $\mathcal{R}$ par $B_{\gamma}$ est le résultat d'une rotation hyperbolique et d'une homothétie.
Les vecteurs propres $\boldsymbol{l}$ et $\boldsymbol{k}$ de $B_{\gamma}$ définissent un cône globalement invariant par cette transformation.
On peut définir un référentiel propre à chaque parabole isochrone $\mathcal{P}$ définie plus haut. Il s'agit du référentiel formé les deux vecteurs unitaires engendrant
respectivement l'axe de symétrie $\mathcal{S}(\mathcal{P})$ de la parabole et sa tangente en l'origine $\mathcal{T}_O (\mathcal{P})$.
On remarque immédiatement que le référentiel propre de la parabole képlerienne est le référentiel canonique $\mathcal{R}$ du plan.
Sur la vidéo ci-dessous on peut constater l'action d'un $\boldsymbol{i}-$Bolst sur cette parabole keplerienne pour $\gamma >1$.
Dès que l'$\boldsymbol{i}-$Bolst démarre, la parabole bolstée (bleue) possède deux intersections
avec l'axe $Oy$ dans le référentiel canonique rouge (celui de la parabole keplerienne), de plus elle est orientée à droite.
Il s'agit donc d'une parabole de Hénon. Par contre elle demeure képlerienne dans son référentiel : c'est la théorie de la relativité isochrone.
Sur la figure ci-dessous on montre comment passer d'une parabole quelconque à une parabole képlerienne.
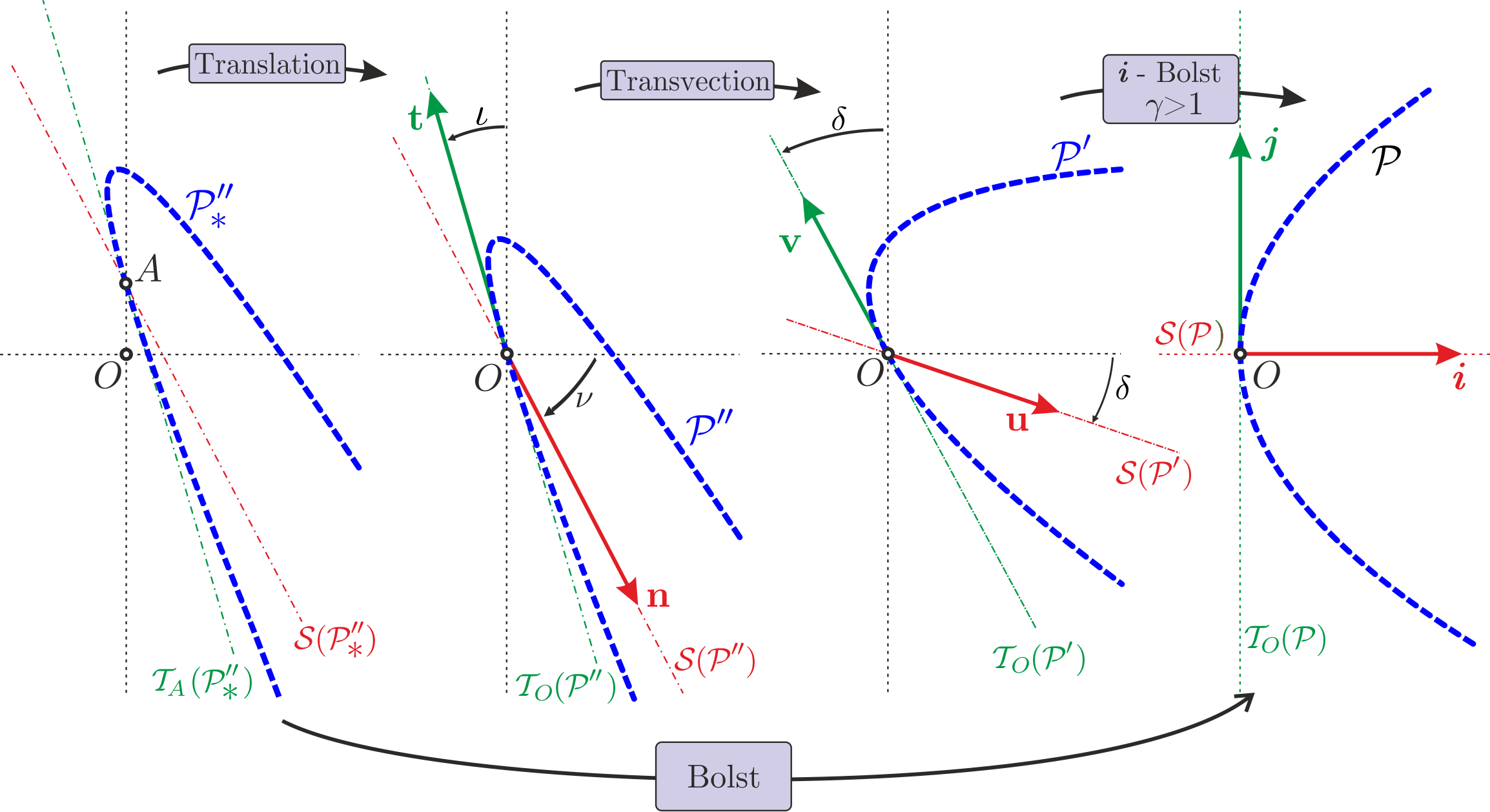
On peut même démontrer qu'une orbite est isochrone si et seulement si elle est l'image par un Bolst d'une orbite képlerienne : l'isochronie est d'essence képlerienne!
Tout comme en relativité restreinte, en isochronie ll existe des intervalles conservés, un temps propre, une écriture des équation de le même façon
dans tous les référentiels, des cones invariants contenant des vecteurs de même propriétés...
Pour terminer ces illustrations nous vous laissons réflechir sur cette vidéo montrant à la fois les paraboles, le mouvement dans le plan $(x,y)$ et les orbites dans les variables
polaires habituelles.
Quelques applications de l'isochronie
La généralisation des lois de Kepler
La relativité isochrone permet de montrer qu'une orbite isochrone est keplerienne dans son référentiel propre. Or nous savons depuis Kepler qu'une telle orbite jouit
d'une propriété tout à fait particulière. Le cube de son demi-grand axe est proportionnel au carré de sa période.
Chaque orbite isochrone dans son potentiel possède un apoastre $r_a$, un périastre $r_p$, une énergie $\xi$ et un moment cinétique $\Lambda$. Cette orbite est périodique
de période $\tau$ et son périastre se déphase de $\Delta \varphi = 2\pi n_p$. Ces paramètres orbitaux sont rassemblés dans le tableau ci-dessous.

La troisième loi de Kepler est vraie pour tous les isochrones !
La théorème de Bertrand
En 1873, Joseph Bertrand montra qu'en dimension 3, les seuls potentiels dans lesquels toutes les orbites bornées non radiales sont fermées sont le keplerien et l'harmonique.
Depuis plusieurs démonstrations ont été produites et le sujet restait toujours d'actualité
(voir ici).
En isochronie, ce thèorème devient un simple corrolaire...
Il est bien connu que la période et le mouvement du périastre sont de simples dérivées partielles de l'action radiale :
\[
\mathcal{A}_r=\frac{1}{\pi}\int_{r_p}^{r_a}\sqrt{2\left[\xi-\psi(r)\right]-\frac{\Lambda^2}{r^2}}dr
\;\;\Longrightarrow\;\;
\left\{
\begin{array}{ccc}
\tau &=& 2\pi \displaystyle\frac{\partial \mathcal{A}_r}{\partial \xi} \\
& & \\
n_p &=& - \displaystyle\frac{\partial \mathcal{A}_r}{\partial \Lambda} \\
\end{array}
\right.
\]
Pour que l'orbite soit fermée, il est nécessaire et suffisant que $n_p$ soit dans $2\pi\mathbb{Q}$.
Sous cette hypothèse, la fonction $(\xi,\Lambda)\mapsto n_p$ est continue de $\mathbb{R}^2\to 2\pi\mathbb{Q}$. Elle est donc constante car $\mathbb{R}\setminus\mathbb{Q}$
est dense dans $\mathbb{R}$. Une simple utilisation du théorème de Schwarz permet alors d'écrire les enchainements suivants :
\[
\frac{\partial n_p}{\partial \xi} =0
\;\;\Longrightarrow\;\;
\frac{\partial^2 \mathcal{A}_r}{\partial \xi\partial \Lambda} =0
\;\;\Longrightarrow\;\;
\frac{\partial \tau}{\partial \Lambda} =0
\]
Pour que l'orbite satisfasse les conditions du théorème de Bertrand il est donc nécessaire que le potentiel soit isochrone.
En inspectant les valeurs possibles du mouvement du périastre,
on constate immédiatement que les seuls potentiels isochrones dont toutes les orbites sont fermées sont bien l'harmonique et le keplerien.
L'isochronie comme un état initial
Dans une étude récente, nous avons montré numériquement que le processus de formation des systèmes autogravitants comme les amas
globulaires ou les galaxies à faible brillance de surface conduisait à un système ischrone bien décrit par le potentiel de Hénon.
La boucle est donc bouclée !
Michel Hénon avait vu juste en 1958, par contre différents processus d'évolution dynamique comme la relaxation à deux corps, les effets de marée galactique, etc.
contribuent à quitter l'état fondamental isochrone. C'est la raison pour laquelle l'observation de tels objets ne revèle plus ce caractère.
Pour les systèmes autogravitants plus complexes comme les galaxies à haute brillance de surface, le processus de formation hierarchique gomme
d'emblée le statut isochrone et revèle in fine de nombreuses propriétés qui restent à éclaircir.