Affiliations

• IMSIA UMR9219
• ENSTA-Paris, Dept of Mechanics, Professor
• Institut Polytechnique de Paris

Research topics

1. Amplification of seismic waves

When seismic waves propaget through alluvial layers or interact with topographic irregularities refraction and scattering phenomena may strongly increase the amplitude of the seismic motion. It thus characterizes the seismic site effects.
At the scale of a sedimentary basin, the analysis of seismic wave propagation is a complex issue: global resonance, propagation in heterogeneous media, generation of surface waves at the basin edges, nonlinear behaviour of surficial layers.

1.1. Modal approaches ↑

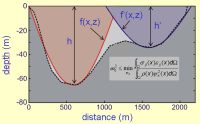
Site effects may be interpreted as a global resonance of the sedimentary layers (Semblat et al., BSSA 2003). Simplified modal approaches, based on the Rayleigh quotient method, have thus been considered (Semblat et al., C.R.Geosciences 2003). Considering admissible modal shapes (Fig.1.), these approaches allow a fast and relaible assessment of the fundamental frequency of geological structures.

Fig.1. Admissible modes for basins (Semblat et al., C.R.Geosc. 2003)

1.2. Wave propagation by the Boundary Element Method ↑

To assess the amplification of seismic waves, it is necessary to simulate their propagation. Various numerical methods may be considered (Semblat & Pecker, 2009): finite differences, finite elements, boundary elements, spectral elements, etc.

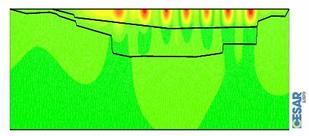
At the scale of a sedimentary basin, the amplification of seismic waves by the surficial depositsis assessed through the (classical) Boundary Element Method for various sites: Nice, Volvi (Fig.2.), Caracas (Semblat et al, SDEE 2005). The geometrical uneveness (topography, (Fig.3.) and the velocity heterogeneities (lithology) play a significant role in the amplification phenomena.

Fig.2. Seismic wave amplification in Volvi (Semblat et al., SDEE 2005)	Fig.3.Scattering by a canyon (Chaillat et al., CMAME 2008)

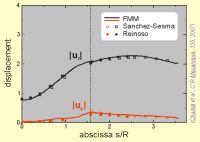
The development of a "fast multipole" BEM formulation in 3D elastodynamics allowed a drastic decrease of the complexity and memory requirements (Chaillat et al., CMAME 2008, GJI 2009). It now allows to perform large three-dimensional problems, Fig.4. (Chaillat et al., CiCP2012), (Meza-Fajardo et al, BSSA 2016).

Fig.4. Scattering by a basin (FM-BEM) (Chaillat et al., GJI 2009)

1.3. Surface waves and time-frequency extraction ↑

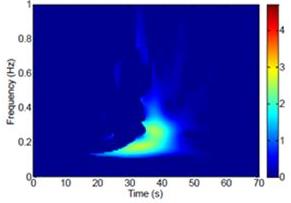
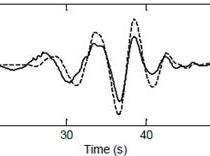
Alluvial basins strongly amplify seismic waves due to basin edge generated surface waves (Fig.4.). In order to assess their contribution to the ground motion, a time-frequency method involving the Stockwell transform has been proposed (Meza-Fajardo et al., BSSA 2015). A normalized inner product allows a more efficient filtering in the time-frequency space (Fig.5., gauche) than the classical approach through the instantaneous reciprocal ellipticity (Fig.5., droite). The application of the proposed method on seismograms recorded during the Chi-chi earthquake has shown its efficiency (Fig.6.).

Fig.5. Filtered time-frequency plots (Meza-Fajardo et al., BSSA 2015)	Fig.6. Filtered time-domain signals for the Chi-chi earthquake

2. Seismic response of soils ↑

2.1. Nonlinear seismic response ↑

In case of strong event, the influence of the nonlinear constitutive properties in the surficial layers is significant. The nonlinear viscoelastic "X-NCQ" model has been developed in order to simultaneously account for the reduction of the shear modulus and the increase of the energy dissipation wrt the distorsion, Fig.7. (Delépine et al., J.Eng.Mech.2009). A so-called 1D-3 components ("1D-3C") approach involving a cyclic elastoplastic multisurface model has also been proposed (Santisi et al., GJI 2012). The 1D-1C and 1D-3C simulations performed for the Tohoku earthquake show the importance of the three-dimensional loading path on the seismic soil response for strong events, Fig.8. (Santisi et al., GJI 2014).

Fig.7. X-NCQ model: attenuation vs shear strain & frequency (Delépine et al., J.Eng.Mech.2009)	Fig.8. 1D-3C nonlinear response for the Tohoku earthquake (Santisi et al., GJI 2014)

2.2. Seismic response and liquefaction of soils ↑

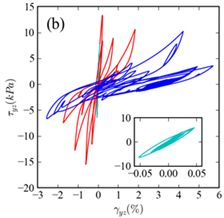
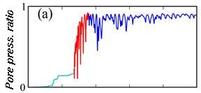
In the case of saturated soils, it is mandatory to account for the pore pressure increase. Iai (1990) proposed a shear modulus correction through a liquefaction front parameter correlated with the normalized shear work. This approach has been extended to multiaxial stress states through 3 components excitations (Santisi et al., GJI 2018). As shown in Fig.9., the hysteresis loops are strongly tilted and enlarged thus leading to a huge decrease of the material strength. The variations of the pore pressure ratio is also a good proxy for the liquefaction process Fig.10.. Furthermore the simplified "X-ELM" approache recently allowed to predict liquefaction triggering for the Urayasu city in Japan (Kteich et al., S&F 2019).

Fig.9. 1D-3C liquefaction front approach (Santisi et al., GJI 2018)	Fig.10. Pore pressure ratio from the 1D-3C liquefaction front approach

3. Soil-structure and site-city interaction ↑

3.1. Macroelement formulation for soil-structure interaction ↑

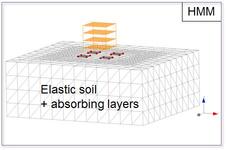
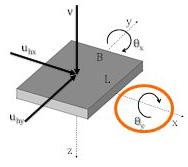
To model soil-structure interaction, we may gather the constitutive nonlinearities of the soil beneath the foundation and at the soil-foundation interface through a macroelement (Abboud Y., PhD 2017). We thus combine the nonlinear constitutive laws between the displacements/rotations and the forces/moments for which the classical theories of elastoplasticty may be applied. The proposed macroelement computes the forces/moments to be applied to the FEM soil model as nodal forces (Fig.11.). It this appears as an original hybride formulation combining a FEM mesh of the soil, to account for the wave radiation, and a macroelement to account for the plastic mechanisms in terms of overturning, sliding and bearing capacity (Fig.12.).

Fig.11. Hybrid macroelement model (Abboud Y., PhD 2017)	Fig.12. Foundation rotation from hybrid macroelement model

3.2. Interaction of seismic waves with a dense building network ↑

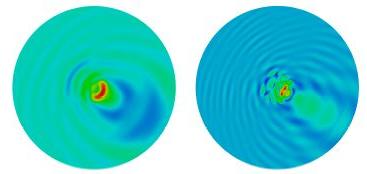
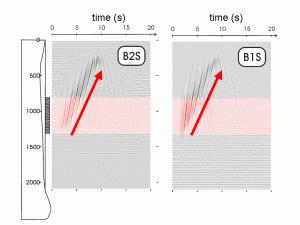
Finally the surface structures may act as secondary seismic sources and influence the seismic "free-field". At larges scales, the interaction between a sedimentary basin and a building network - so-called site-city interaction - is assessed numerically (Fig.13.). The coincidence between the fundamental frequencies of the structures and the resonance frequency of the basin controls site-city interaction. The coherency of the wavefield, the effects of the urban density and the building heterogeneity are also discussed (Fig.14.).

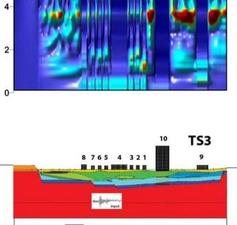
Fig.13. Site-city interaction in Nice (Kham et al., BSSA 2008)	Fig.14. Site-city interaction in Rome (Varone et al., SDEE 2019)