Affiliations

I am currently an Associate Professor at the Institute of Mechanical Sciences and Industrial Applications (IMSIA UMR 9219) of ENSTA Paris. ENSTA Paris is a member of the Institut Polytechnique de Paris

You can also visit my Researchgate and HAL profiles to obtain more information on my research activities.

Research topics

1. Noise generation mechanisms in the context of rotating machines

Context open rotors: wind turbines, marine propellers, ...

1.1 Experimental characterization of dynamic stall noise

Funding DGA AEROAC and ANR PIBE (Prédire l'Impact du Bruit des Eoliennes).
Postdoc David Raus (2019-2021) and PhD thesis Lisa Sicard (2020-...) Collaboration with Michel Roger, Emmanuel Jondeau and Pascal Souchotte of LMFA at Ecole Centrale de Lyon.

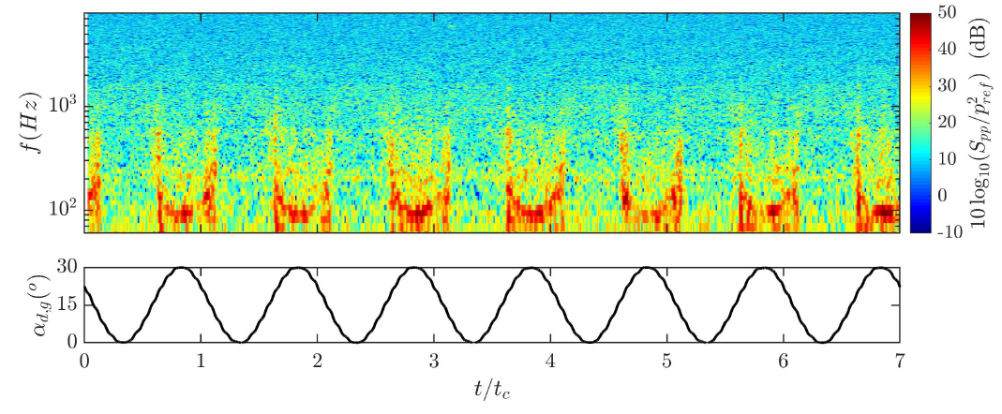
Dynamic stall noise measurement setup in the anechcoic chamber of Ecole Centrale de Lyon	Spectrogram of the noise for a NACA 0012 airfoil oscillating at a frequency of 0.66Hz between 0 and 30 degrees (means angle of attack of 15 degrees, Reynolds of 200,000)

1.2 Wind Turbine Noise Modeling Based on Amiet's Theory

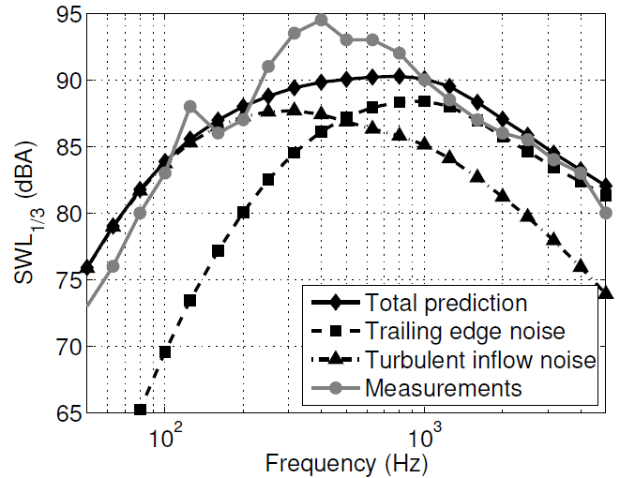
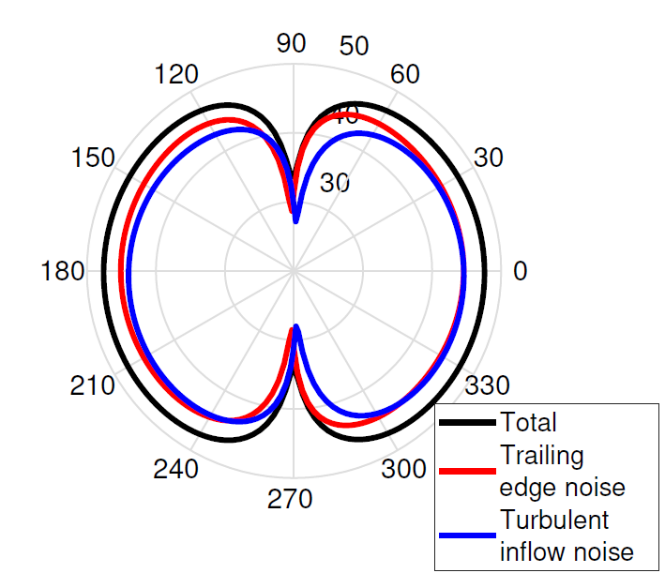
PhD thesis of Yuan Tian (MESR 2012-2016)

Trailing edge noise and turbulent inflow noise - Effects of wind shear and atmospheric turbulence

Third octave band spectrum of sound power level meaured by DTU and calculated (left), and horizontal directivity of wind turbine overall sound pressure level (right) in a neutral atmosphere (Tian and Cotté, 2016)

2. Long range atmospheric propagation of wind turbine noise

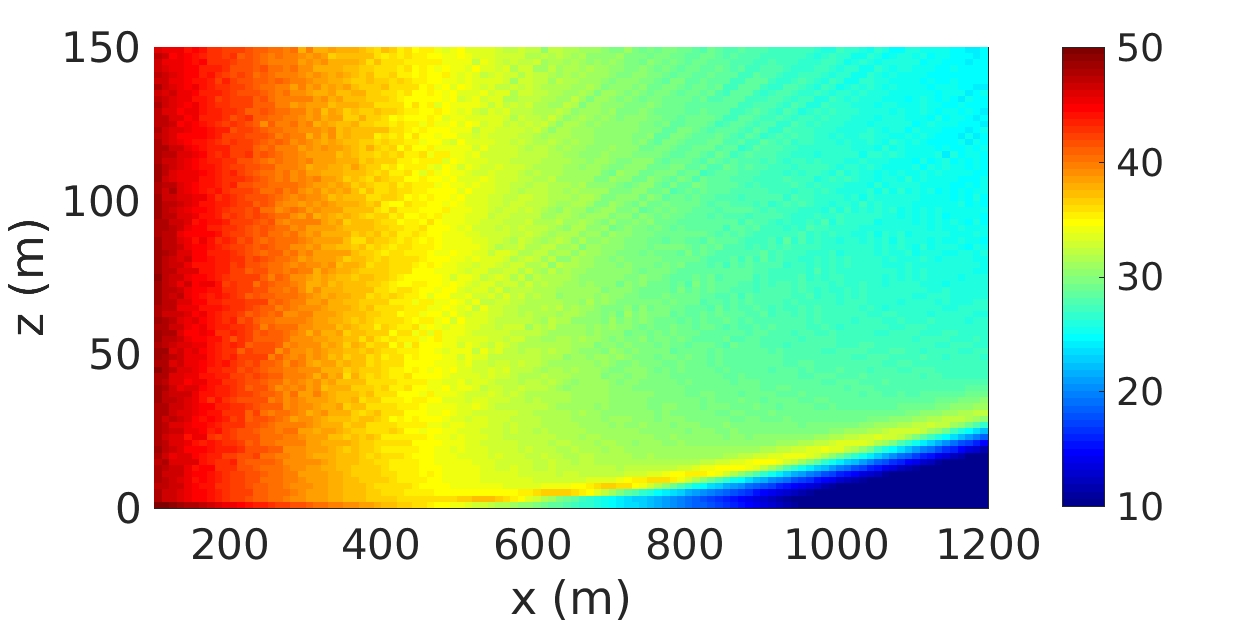
2.1 Extended source model for wind turbine noise

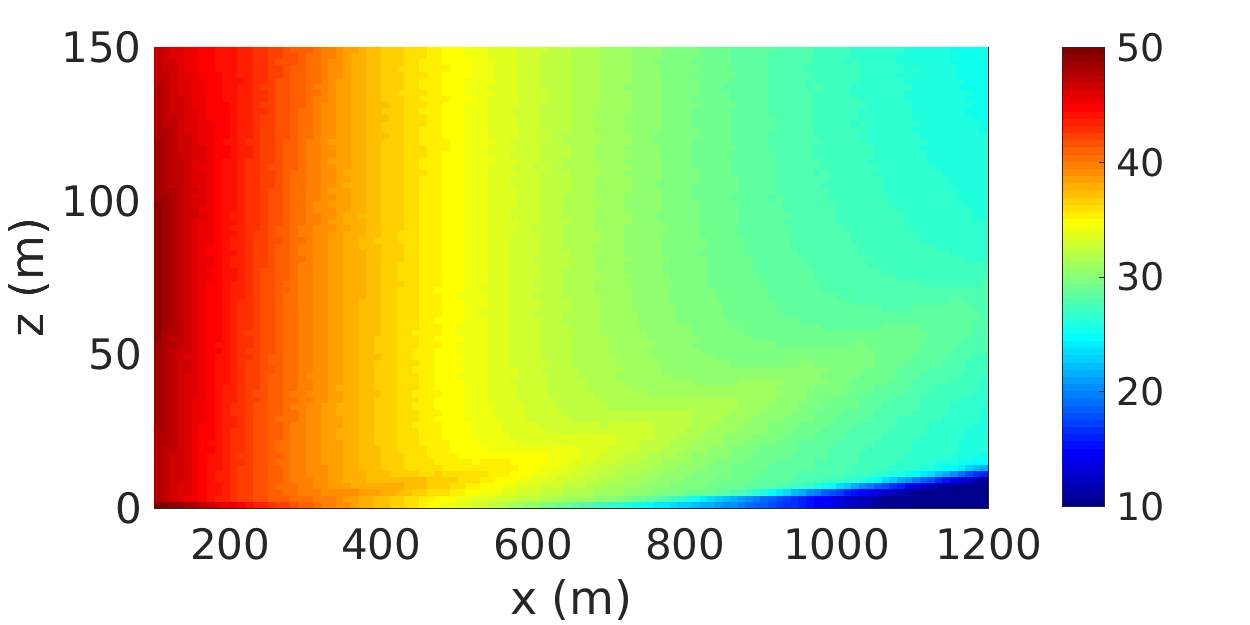
Need to account for the motion of the blades and to the source to correctly predict the amplitude modulation of wind turbine noise. Also, the size of the shadow zone is overpredicted when the point source approximation is used.

Maps of the overall sound pressure level with the Amiet-PE extended source model (left) and with the pouint source approximation (right) in a neutral atmosphere (Cotté, 2019)

2.2 Auralization of wind turbine noise

PhD thesis of David Mascarenhas (2020-...) within the ITN VRACE (Virtual Reality Audio for Cyber Environments).

3. Vibroacoustics and sound synthesis of musical instruments

3.1 Computer-aided design of piano soundboards (MAESSTRO project)

Funding ANR: visit project website at https://www.maesstro.cnrs.fr/

Postdoc Benjamin Elie (2019)

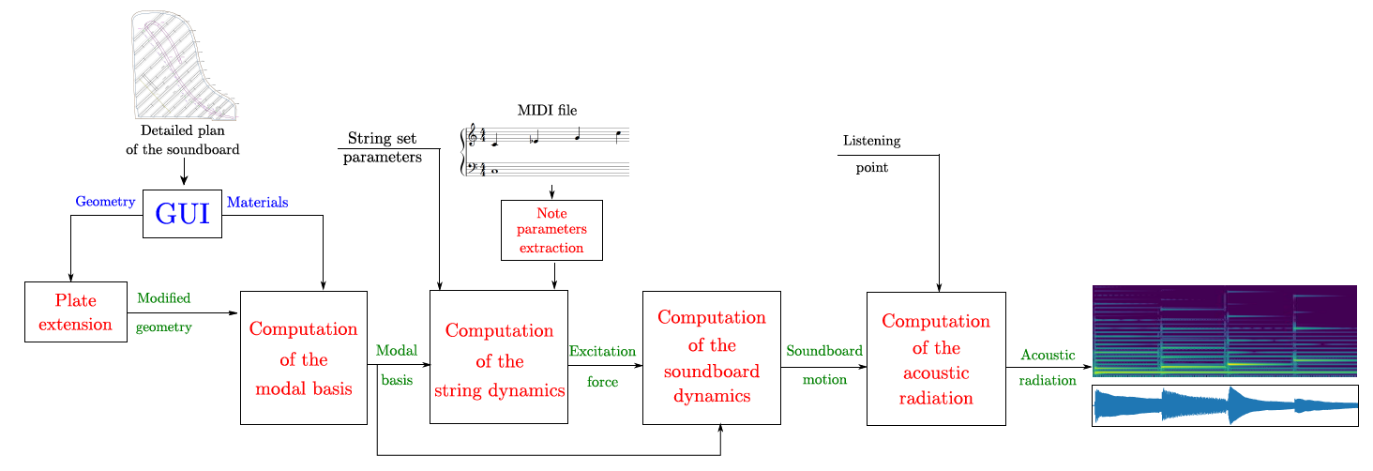
Block-diagram of the MAESSTRO software architecture. (Elie et al., ISMA 2019)

3.2 Time-domain damping models for transient vibroacoustic response prediction and sound synthesis using digital filters

Funding DGA
Postdoc Augustin Parret-Fréaud (2014-2016)

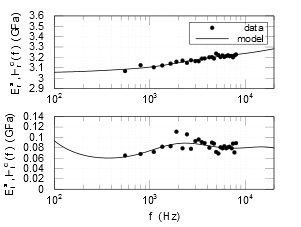
Real and imaginary parts of the complex Young's modulus measured by Collet et al. (2013) and of the associated digital filter response (Parret-Fréaud et al., MSSP 2016)

3.3 Vibroacoustics and sound synthesis of the piano Collaboration with Antoine Chaigne and Roberto Viggiano

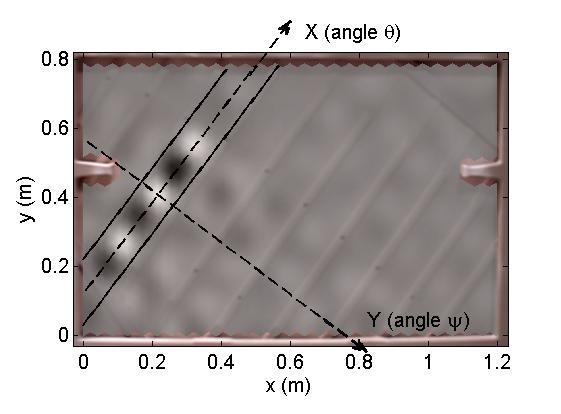
Example of vibration localization measured on an upright piano soundboard (Chaigne et al., J. Acoust. Soc. Am. 2013)

The development of a "fast multipole" BEM formulation in 3D elastodynamics allowed a drastic decrease of the complexity and memory requirements (Chaillat et al., CMAME 2008, GJI 2009). It now allows to perform large three-dimensional problems, Fig.4. (Chaillat et al., CiCP2012), (Meza-Fajardo et al, BSSA 2016).

Fig.4. Scattering by a basin (FM-BEM) (Chaillat et al., GJI 2009)

1.3. Surface waves and time-frequency extraction ↑

Alluvial basins strongly amplify seismic waves due to basin edge generated surface waves (Fig.4.). In order to assess their contribution to the ground motion, a time-frequency method involving the Stockwell transform has been proposed (Meza-Fajardo et al., BSSA 2015). A normalized inner product allows a more efficient filtering in the time-frequency space (Fig.5., gauche) than the classical approach through the instantaneous reciprocal ellipticity (Fig.5., droite). The application of the proposed method on seismograms recorded during the Chi-chi earthquake has shown its efficiency (Fig.6.).

Fig.5. Filtered time-frequency plots (Meza-Fajardo et al., BSSA 2015)	Fig.6. Filtered time-domain signals for the Chi-chi earthquake

2. Seismic response of soils ↑

2.1. Nonlinear seismic response ↑

In case of strong event, the influence of the nonlinear constitutive properties in the surficial layers is significant. The nonlinear viscoelastic "X-NCQ" model has been developed in order to simultaneously account for the reduction of the shear modulus and the increase of the energy dissipation wrt the distorsion, Fig.7. (Delépine et al., J.Eng.Mech.2009). A so-called 1D-3 components ("1D-3C") approach involving a cyclic elastoplastic multisurface model has also been proposed (Santisi et al., GJI 2012). The 1D-1C and 1D-3C simulations performed for the Tohoku earthquake show the importance of the three-dimensional loading path on the seismic soil response for strong events, Fig.8. (Santisi et al., GJI 2014).

Fig.7. X-NCQ model: attenuation vs shear strain & frequency (Delépine et al., J.Eng.Mech.2009)	Fig.8. 1D-3C nonlinear response for the Tohoku earthquake (Santisi et al., GJI 2014)

2.2. Seismic response and liquefaction of soils ↑

In the case of saturated soils, it is mandatory to account for the pore pressure increase. Iai (1990) proposed a shear modulus correction through a liquefaction front parameter correlated with the normalized shear work. This approach has been extended to multiaxial stress states through 3 components excitations (Santisi et al., GJI 2018). As shown in Fig.9., the hysteresis loops are strongly tilted and enlarged thus leading to a huge decrease of the material strength. The variations of the pore pressure ratio is also a good proxy for the liquefaction process Fig.10.. Furthermore the simplified "X-ELM" approache recently allowed to predict liquefaction triggering for the Urayasu city in Japan (Kteich et al., S&F 2019).

Fig.9. 1D-3C liquefaction front approach (Santisi et al., GJI 2018)	Fig.10. Pore pressure ratio from the 1D-3C liquefaction front approach

3. Soil-structure and site-city interaction ↑

3.1. Macroelement formulation for soil-structure interaction ↑

To model soil-structure interaction, we may gather the constitutive nonlinearities of the soil beneath the foundation and at the soil-foundation interface through a macroelement (Abboud Y., PhD 2017). We thus combine the nonlinear constitutive laws between the displacements/rotations and the forces/moments for which the classical theories of elastoplasticty may be applied. The proposed macroelement computes the forces/moments to be applied to the FEM soil model as nodal forces (Fig.11.). It this appears as an original hybride formulation combining a FEM mesh of the soil, to account for the wave radiation, and a macroelement to account for the plastic mechanisms in terms of overturning, sliding and bearing capacity (Fig.12.).

Fig.11. Hybrid macroelement model (Abboud Y., PhD 2017)	Fig.12. Foundation rotation from hybrid macroelement model

3.2. Interaction of seismic waves with a dense building network ↑

Finally the surface structures may act as secondary seismic sources and influence the seismic "free-field". At larges scales, the interaction between a sedimentary basin and a building network - so-called site-city interaction - is assessed numerically (Fig.13.). The coincidence between the fundamental frequencies of the structures and the resonance frequency of the basin controls site-city interaction. The coherency of the wavefield, the effects of the urban density and the building heterogeneity are also discussed (Fig.14.).

Fig.13. Site-city interaction in Nice (Kham et al., BSSA 2008)	Fig.14. Site-city interaction in Rome (Varone et al., SDEE 2019)