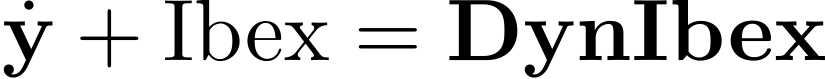DynIbex is a plug-in of Ibex library which is a library for constraint processing over real numbers.
DynIbex offers a set of validated numerical integration methods based on Runge-Kutta schemes to solve initial value problem of ordinary differential equations and for DAE in Hessenberg index 1 form.
- We consider an ordinary differential equation with a given initial condition, that is an initial value problem (IVP) \[ \dot{\mathbf{y}}(t) = f(t, \mathbf{y}(t)) \quad \text{with}\quad \mathbf{y}(0)= \mathbf{y}_0\] with \(f : \mathbb{R} \times \mathbb{R}^n \to \mathbb{R}^n\) is assumed to be continuous \(t\) and globally Lipschitz in \(\mathbf{y}\). Solving an IVP consists in finding a function \(\mathbf{y}(t)\) described by the ODE and satisfying the initial condition. The solution of an IVP is denoted by \(\mathbf{y}(t;\mathbf{y}_0)\). A standard numerical integration method computes a sequence of values \((t_n, \mathbf{y}_n)_{n\in\mathbb{N}}\) approximating the solution \(\mathbf{y}(t;\mathbf{y}_0)\) of an IVP such that \(\mathbf{y}_n \approx \mathbf{y}(t_n;\mathbf{y}_{n-1})\). The goal of a validated or guaranteed numerical integration method is to compute the sequence of boxes \((t_n, [\mathbf{y}_n])_{n\in\mathbb{N}}\) such that \([\mathbf{y}_n] \supseteq \mathbf{y}(t_n;[\mathbf{y}_{n-1}]) = \{ \mathbf{y}(t_n;\mathbf{y}_{n-1}) : \forall \mathbf{y}_{n-1} \in [\mathbf{y}_{n-1}] \}\).
- We also consider a differential-algebraic equations in Hessenberg index 1 form with consistent initial conditions, that IVP of the form \[ \begin{align*} \dot{\mathbf{y}}(t) & = f (t, \mathbf{y}(t), \mathbf{x}(t)) \\ 0 & = g(t, \mathbf{y}(t), \mathbf{x}(t)) \end{align*} \quad\text{with}\quad \mathbf{y}(0) = \mathbf{y}_0\quad\text{and}\quad \mathbf{x}(0) = \mathbf{x}_0 \] with \(f : \mathbb{R} \times \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n\) is assumed to be continuous \(t\) and globally Lipschitz in \(\mathbf{y}\), and \(g : \mathbb{R} \times \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}\). Solving an IVP consists in finding two functions \(\mathbf{y}(t)\) and \(\mathbf{x}(t)\) described by the DAE and satisfying the initial conditions. The solutions of an IVP for DAE is denoted by \(\mathbf{y}(t;\mathbf{y}_0)\) and \(\mathbf{x}(t;\mathbf{x}_0)\). Once again, the goal of a validated or guaranteed numerical integration method is to compute two sequences of boxes \((t_n, [\mathbf{y}_n])_{n\in\mathbb{N}}\) and \((t_n, [\mathbf{x}_n])_{n\in\mathbb{N}}\) such that \([\mathbf{y}_n] \supseteq \mathbf{y}(t_n;[\mathbf{y}_{n-1}]) = \{ \mathbf{y}(t_n;\mathbf{y}_{n-1}) : \forall \mathbf{x}_{n-1} \in [\mathbf{x}_{n-1}] \}\) and \([\mathbf{x}_n] \supseteq \mathbf{x}(t_n;[\mathbf{x}_{n-1}]) = \{ \mathbf{x}(t_n;\mathbf{x}_{n-1}) : \forall \mathbf{x}_{n-1} \in [\mathbf{x}_{n-1}] \}\)
Contributors
Julien Alexandre dit Sandretto, Alexandre Chapoutot, Olivier MullierSponsors
This research benefited from the support of the "Chair Complex Systems Engineering - Ecole Polytechnique, THALES, DGA, FX, DASSAULT AVIATION, DCNS Research, ENSTA ParisTech, Télécom ParisTech, Fondation ParisTech and FDO ENSTA"Features
- We can solve IVP for ODE and DAE in Hessenberg index 1 form
- Implement different Runge-Kutta methods:
- Heun's method,
- Midpoint method,
- Kutta 3 (order 3),
- Radau-IIA (order 3 and order 5),
- RK4,
- Lobatto-IIIA (order 4),
- Lobatto-IIIC (order 4)
- Gauss-Legendre (order 4 and order 6).
- With affine arithmetic, uncertain ODE can be considered without putting parameters in the state-vector (QR-method is not used)
- Two algorithms to compute LTE are implemented: one based on symbolic differentiation and one based on automatic differentiation (see our article)
- Some methods to verify properties on tubes computed by guaranteed Runge-Kutta methods are available to embed this library into contractor programming framework (see our article)
How to cite DynIBEX
You should cite our paper published in Reliable Computing Journal with the following bibtex entry
@Article{Sandretto:2016:VEI,
Title = {Validated Explicit and Implicit {R}unge--{K}utta Methods},
Author = {Julien Alexandre {dit Sandretto} and Alexandre Chapoutot},
Journal = {Reliable Computing},
Year = {2016},
Month = {Jul},
Number = {1},
Pages = {79--103},
Volume = {22}
}
History on Interval Runge-Kutta
This work on validated Runge-Kutta methods takes its roots in two previous works:- GRKlib by Olivier Bouissou and Matthieu Martel which defined a validated version of the classical RK4 methods
- The extension to deal with any explicit Runge-Kutta methods as defined in the article published at NASA Formal Methods 2013 written by Olivier Bouissou, Alexandre Chapoutot and Adel Djoudi.
- Andrzej
Marciniak et alii work on this topic
since 1999
We go a step forward with our approach by bringing an algorithmic answer to the remark found in the survey article saying that the LTE cannot be written in general form for an arbitrary order.
- Michael Hartmann and Knut Petras at ICIAM 1999 presented some work on this topic but we cannot find no more than 5 lines in an abstract (more information is welcomed).
DOWNLOAD and INSTALLATION
DynIbex is made of two main ingredients: an extension of the affine arithmetic and the validated Runge-Kutta methods. Current version 2.3 (February 2025)
- Download the DynIbex source code, now embedded in source code of Ibex 2.1.17
- Note that you need Python 2.7 for the installation
- You can access to a small API of DynIbex.
Put the archive into the Ibex directory, then write the following commands:
~/Ibex/$ tar xvfz dynibex-2.3.tar.gz ~/Ibex/$ cd dynibex-2.3 ~/Ibex/dynibex-2.3/$ ./waf configure [options] ~/Ibex/dynibex-2.3/$ sudo ./waf install
Publications on DynIBEX
Theory of validated Runge-Kutta methods
- Validated Explicit and Implicit Runge-Kutta Methods Julien Alexandre Dit Sandretto, Alexandre Chapoutot Reliable Computing electronic edition, 2016, Special issue devoted to material presented at SWIM 2015, 22.
- Validated Simulation of Differential Algebraic Equations with Runge-Kutta Methods Julien Alexandre Dit Sandretto, Alexandre Chapoutot Reliable Computing electronic edition, 2016, Special issue devoted to material presented at SWIM 2015, 22.
- Runge-Kutta Theory and Constraint Programming, Julien Alexandre Dit Sandretto, Alexandre Chapoutot International Symposium on Scientific Computing, Computer Arithmetics and Verified Numerics, Sep 2016, uppsala, Sweden.
- Contraction, propagation and bisection on a validated simulation of ODE, Julien Alexandre Dit Sandretto, Alexandre Chapoutot Summer Workshop on Interval Methods, Jun 2016, Lyon, France.
- DynBEX: a Differential Constraint Library for Studying Dynamical Systems, Julien Alexandre Dit Sandretto, Alexandre Chapoutot Conference on Hybrid Systems: Computation and Control, Poster, Vienne, Austria. 2016.
- Validated Computation of the Local Truncation Error of Runge-Kutta Methods with Automatic Differentiation, Olivier Mullier, Alexandre Chapoutot, Julien Alexandre Dit Sandretto. Optimization Methods and Software, Taylor & Francis, 2018.
Applications using DynIBEX
- Tuning PI controller in nonlinear uncertain closed-loop systems with interval analysis
- Viability kernel computation based on interval methods
It is used in ViabIBEX Software - Control of Nonlinear Switched Systems Based on Validated Simulation, Adrien Le Coent, Julien Alexandre Dit Sandretto, Alexandre Chapoutot, Laurent Fribourg International Workshop on Symbolic and Numerical Methods for Reachability Analysis, Apr 2016, Vienne, Austria. 2016
- Appropriate Design Guided by Simulation: An Hovercraft Application, Julien Alexandre Dit Sandretto, Douglas Piccani de Souza, Alexandre Chapoutot 2016
- Robust Motion Planning Based on Sliding Horizon and Validated Simulation Elliot Brendel, Julien Alexandre Dit Sandretto, Alexandre Chapoutot 10th Summer Workshop on Interval Methods, and 3rd International Symposium on Set Membership - Applications, Reliability and Theory, Jun 2017, Manchester, United Kingdom
- Formal Verification of Robotic Behaviors in Presence of Bounded Uncertainties Julien Alexandre Dit Sandretto, Alexandre Chapoutot, Olivier Mullier First IEEE International Conference on Robotic Computing, Apr 2017, Taichung, Taiwan
- BoxRRT* -A Reliable Motion Planner Adina Panchea, Alexandre Chapoutot, David Filliat 10th Summer Workshop on Interval Methods, and 3rd International Symposium on Set Membership - Applications, Reliability and Theory, Jun 2017, Manchester, United Kingdom
- Extended Reliable Robust Motion Planners Adina Panchea, Alexandre Chapoutot, David Filliat 56th IEEE Conference on Decision and Control, Dec 2017, Melbourne, Australia. IEEE, 2017
- An Improved Algorithm for the Control Synthesis of Nonlinear Sampled Switched Systems Adrien Le Coënt, Julien Alexandre Dit Sandretto, Alexandre Chapoutot, Laurent Fribourg Formal Methods in System Design, Springer Verlag, 2017
- Formal Verification of Robotic Behaviors in Presence of Bounded Uncertainties Julien Alexandre Dit Sandretto, Alexandre Chapoutot, Olivier Mullier Journal of Software Engineering for Robotics, 2017, 8 (1), pp.78-88.
- Reliable motion planner evaluated on a mobile robot Pierre-André Crépon, Adina Panchea, Alexandre Chapoutot International Workshop on New Frontiers in Computational Robotics, Jan 2018, Laguna Hills, California, United States. 2018,
- Reliable NonLinear Model-Predictive Control via Validated Simulation Julien Alexandre dit Sandretto, ACC, Milwaukee, USA 2018
- An Interval-based Sliding Horizon Motion Planning Method Julien Alexandre dit Sandretto, Elliot Brendel, and Alexandre Chapoutot, ADHS 2018
Validated Runge-Kutta methods for ODE (Research report and Article)
Description
A Runge-Kutta method, starting from an initial value \(\mathbf{y}_n\) at time \(t_n\) and a finite time horizon \(h\), the step-size, produces an approximation \(\mathbf{y}_{n+1}\) at time \(t_{n+1}\), with \(t_{n+1}-t_n = h\), of the solution \(\mathbf{y}(t_{n+1}; \mathbf{y}_n)\). Furthermore, to compute \(\mathbf{y}_{n+1}\), a Runge-Kutta method computes \(s\) evaluations of \(f\) at predetermined time instants. The number \(s\) is known as the number of stages of a Runge-Kutta method. More precisely, a Runge-Kutta method is defined by \[ \mathbf{y}_{n+1} = \mathbf{y}_n + h \sum_{i=1}^{s}b_i \mathbf{k}_i\enspace, \] with \(\mathbf{k}_i\) defined by \[ \mathbf{k}_i = f\left(t_0 + c_i h, \mathbf{y}_n + h \sum_{j=1}^{s} a_{ij}\mathbf{k}_j \right)\enspace. \] The coefficient \(c_i\), \(a_{ij}\) and \(b_i\), for \(i,j=1,2,\cdots, s\), fully characterize the Runge-Kutta methods and their are usually synthesized in a Butcher tableau of the form as follows: \[ \begin{array}{c|cccc} c_1 & a_{11} & a_{12} & \dots & a_{1s}\\ c_2 & a_{21} & a_{22} & \dots & a_{2s}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ c_s & a_{s1} & a_{s2} & \dots & a_{ss} \\ \hline & b_1 & b_2 & \dots & b_s\\ \end{array} \] In function of the form of the matrix \(A\), made of the coefficients \(a_{ij}\), a Runge-Kutta method can be- explicit the computation of an intermediate \(k_i\) only depends on the previous steps \(k_j\) for \(j < i\);
- diagonally implicit the computation of an intermediate step \(k_i\) involves the value \(k_i\) and so non-linear systems in \(k_i\) must be solved;
- fully implicit the computation of intermediate steps involves the solution of a non-linear system of equations in all the values \(k_i\) for \(i=1,2,\cdots,s\).
Example: basic integration
This example shows the simple way to solve IVP with DynIbex.- To see the source code of this example
- To download the source code of this example
Validated Runge-Kutta methods for DAE (Article)
Description
The validated numerical integration of DAE in Hessenberg index 1 form can be also based on Runge-Kutta scheme. Nevertheless, it implies the definition of a new operator for the computation of the a priori enclosure. For more details, see the article.Example: a simple DAE
- To see the source code of this example
- To download the source code of this example
Towards a contractor programming with differential equations
Description
This example has been written with the help of Gilles Chabert. It demonstrates the ability to embed validated Runge-Kutta methods for ODE into the contractor programming framework. Nevertheless, more work has to be done to have a complete and robust framework of constraint programming techniques with differential equations.Example: a simple forward-backward operator for ODEs.
- To see the source code of this example
- To download the source code of this example
Simulation of a car in open loop, continuous-time closed loop and sampled closed loop
Description
We consider a simple nonlinear dynamics of a car given by equations \[ \begin{aligned} \dot{v}(t) & = \frac{ -50.0 v - 0.4 v^2}{m} \\ & \text{with}\quad m \in [990,1010] \end{aligned} \]Example: open loop system
- To see the source code of this example
- To download the source code of this example
Example: continuous closed loop system with PI controller
- We increase the dimension of the dynamical system to embed the integral part of the PI controller \[ \begin{pmatrix} \dot{v} \\ \dot{w} \end{pmatrix} = \begin{pmatrix} \frac{k_p (10.0 - v) + k_i w -50.0v - 0.4v^2}{m} \\ 10.0 - v \end{pmatrix} \quad\text{with}\quad m\in[990, 1010], k_p=1440, k_i=35 \] The control input is \(10\)
- To see the source code of this example
- To download the source code of this example
Example: continuous closed loop system with PI controller with safety property
- We want to check that \(\forall t \in[0, 10], v(t) \in [0,11]\)
- To see the source code of this example
- To download the source code of this example
Example: closed loop system with discretized PI controller
- To see the source code of this example
- To download the source code of this example
Validated Runge-Kutta methods for dynamical systems with state constraints
Description
The validated numerical integration of dynamical systems with state constraints is available. It combines validated Runge-Kutta scheme with contractor operators to ensure the respect of constraints.Example: a simple Production-Destruction systems
- To see the source code of this example
- To download the source code of this example
Cosimulation of Dynamical Systems
Description
These examples demonstrate the ability to solve coupled dynamical systems using cosimulation approach. First example is related to the heating of 8 rooms appartment and second example is related to linked springs.Example 1: 8 rooms
- To see the source code of this example
- To download the source code of this example
Example 2: Springs
- To see the source code
- To download the source code of this example
Checking a Signal Temporal Logic (STL) formula
Description
This example shows how to check an STL formula on the result of a simulation. A simple 1D-linear system is simulated and we check if the system stay under a value until it reaches this value.Example
- To see the source code of this example
- To download the source code of this example