Quelques précisions sur les Univers homogènes et isotropes
Les
solutions des équations de la relativité
générale dans le contexte d'un Univers homogène et
anisotrope (Univers de Bianchi) forment un ensemble de problèmes
passionant et suffisament méconnu pour que nous y consacrions
quelques lignes ....
Équations d'Einstein
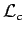 décrit
l'état de courbure de l'Univers et l'autre
décrit
l'état de courbure de l'Univers et l'autre
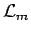 décrit l'énergie impulsion présente dans
l'Univers, nous avons ainsi
décrit l'énergie impulsion présente dans
l'Univers, nous avons ainsi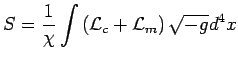 |
(1) |
Le terme
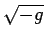 , racine
carrée du déterminant de la métrique
considérée.
, racine
carrée du déterminant de la métrique
considérée.
Dans la relativité générale d'Einstein, le lagrangien de courbure est simplement le scalaire de courbure,
| (2) |
trace du tenseur de Ricci, double contraction du tenseur de courbure de Riemann
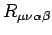
| (3) |
La densité de lagrangien de matière dépend directement de la nature de celle ci. C'est à partir de
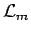 que l'on forme le
tenseur énergie-impulsion
que l'on forme le
tenseur énergie-impulsion
![$\displaystyle T_{\mu\nu}=2\,\left[ \dfrac{\partial\mathcal{L}_{m}}{\partial g^{\mu\nu}
}-\dfrac{1}{2}g_{\mu\nu}\mathcal{L}_{m}\right]$](img8.gif) |
(4) |
Le minimum de l'action
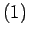 pour des variations
de la métrique est atteint pour les équations d'Einstein
pour des variations
de la métrique est atteint pour les équations d'Einstein
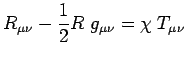 |
(5) |
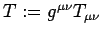 ,
une ligne de
calcul donne
,
une ligne de
calcul donne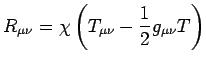 |
(6) |
La constante de couplage est obtenue par limite en champ faible de la théorie, on trouve
| (7) |
Univers de Bianchi
| (8) |
Les classes d'équivalence des espacetemps homogènes en dimension 3+1 s'obtiennent en considérant les classes d'équivalences des constantes de structure
Il est commode de décomposer ces constantes en une partie symétrique et une partie antisymétrique. Ceci est toujours possible en écrivant
| (9) |
où
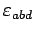 est
le tenseur unité complètement
antisymétrique et
est
le tenseur unité complètement
antisymétrique et
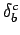 le
symbole de Kronecker,
le
symbole de Kronecker, | (10) |
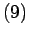 permet de voir clairement
qu'il existe neuf types distincts d'espaces homogènes en
dimension 3+1.
Six proviennent des 6 degrés de libertés introduits par
les six
composantes indépendantes du tenseur symétrique
permet de voir clairement
qu'il existe neuf types distincts d'espaces homogènes en
dimension 3+1.
Six proviennent des 6 degrés de libertés introduits par
les six
composantes indépendantes du tenseur symétrique ![$\displaystyle N^{ab}=\left[
\begin{array}[c]{lll}
n_{1} & 0 & 0\\
0 & n_{2} & 0\\
0 & 0 & n_{3}
\end{array}
\right]$](img27.gif) |
(11) |
Toujours dans cette base, et sans restreindre la généralité de notre propos, la relation
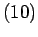 permet de poser
permet de poser
![$ Z_{b}=\left[ a,0,0\right] $](img29.gif) pourvu que
pourvu que
| (12) |
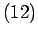
| Propriétés de |
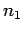 |
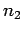 |
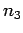 |
Modèle | |
| 0
est valeur propre triple de |
0 | 0 | 0 | 0 |
|
| 0 | 0 | 0 |
|
||
| 0
est valeur propre double de |
0 | 0 | 0 |
|
|
| 0 | 0 |
|
|||
| 0
est valeur propre simple de |
0 | 0 |
|
||
| 0 |
|
||||
| 0 | 0 |
|
|||
| 0 |
|
||||
| 0 |
|
||||
| 0
n'est pas valeur propre de |
0 |
|
|||
| 0 |
|
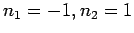 ,
, 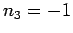 et
donc forcément
et
donc forcément 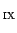 avec une signature + et 0 hors du
spectre. Nous retrouvons bien les neuf cas distincts d'espaces
riemanniens
homogènes de dimension 3. Les chiffres romains associés
aux types
indiqués correspondent à la classification faite par L.
Bianchi en
1898.
avec une signature + et 0 hors du
spectre. Nous retrouvons bien les neuf cas distincts d'espaces
riemanniens
homogènes de dimension 3. Les chiffres romains associés
aux types
indiqués correspondent à la classification faite par L.
Bianchi en
1898.
Une fois les espaces homogènes classifiés, il est possible dans chaque cas d'écrire le tenseur métrique associé et d'en déduire les composantes du tenseur de Ricci.
Formulation BKL (Belinski, Khalatnikov, Lifchitz)
On
peut prouver qu'il existe toujours une famille de fonctions (
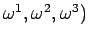 ,
un temps conforme
,
un temps conforme ![]() tel que
tel que 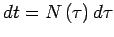 et
et 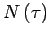 une fonction
''lapse'' telle que
une fonction
''lapse'' telle que
| (13) |
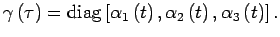
On
peut ainsi expliciter les équations d'Einstein : En
considérant que
l'Univers est remplis d'un d'un fluide parfait, de pression ![]() de densité
d'énergie
de densité
d'énergie 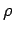 et
décrit par un champ de quadrivitesse de composante
covariante
et
décrit par un champ de quadrivitesse de composante
covariante 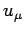 au
repos dans le référentiel synchrone
(
au
repos dans le référentiel synchrone
(
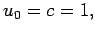
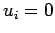 )
)
| (14) |
On considère généralement que ce fluide est barotropique. C'est-à-dire qu'il suit une équation d'état de la forme
| (15) |
![$ \Gamma\in\left[ 0,2\right] $](img68.gif) est la constante barotropique. Une telle
relation est très générale et s'applique à
de nombreux fluides
pour peu qu'ils contiennent une phase dominante.
est la constante barotropique. Une telle
relation est très générale et s'applique à
de nombreux fluides
pour peu qu'ils contiennent une phase dominante.
En
considérant une fonction lapse égale au volume de
l'Univers :
![]() (
(
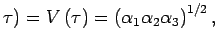 les
équations de la dynamique de l'Univers
homogène et anisotrope deviennent
les
équations de la dynamique de l'Univers
homogène et anisotrope deviennent
ou l'on a noté
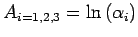 ,
,
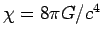 ,
,
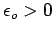 si
si
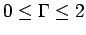 et
et
| (17) | |
Formulation Hamiltonienne
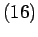 est séparée :
d'un coté des termes dérivés, "cinétique" (
est séparée :
d'un coté des termes dérivés, "cinétique" (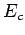 ),
de
l'autre des termes non dérivés
),
de
l'autre des termes non dérivés 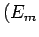 et
et
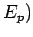 .
Le terme
cinétique est une forme quadratique, elle se diagonalise par un
changement
de variable linéaire
.
Le terme
cinétique est une forme quadratique, elle se diagonalise par un
changement
de variable linéaire
![\begin{displaymath}
M:=\left[
\begin{array}[c]{ccc}
\frac{1}{\sqrt{2}} & \fra...
...\;A_{3}^{\prime}\right] ^{T}=\mathbf{q}^{\prime}
\end{array}
\end{displaymath}](img83.gif)
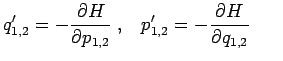 et et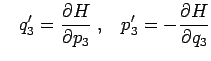 |
(18) |
avec
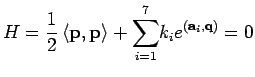
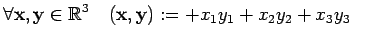 et
et 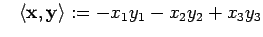 |
(19) |
les constantes
![\begin{displaymath}
\begin{array}[c]{ccc}
k_{1}:=2n_{1}n_{2} & k_{2}:=2n_{1}n_...
...& k_{6}:=-n_{3}^{2}\\
& k_{7}=-4\rho_{o}\chi &
\end{array}
\end{displaymath}](img89.gif)
![\begin{displaymath}
\begin{array}[c]{ccc}
\mathbf{a}_{1}{\scriptsize :=[0,}\fr...
...{\,({2}-\,\Gamma)\sqrt{6}}
{4}{\scriptsize ]} &
\end{array}
\end{displaymath}](img90.gif)
dont la projection orthognale sur le plan
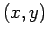 laisse entrevoir des
applications géométriques ...
laisse entrevoir des
applications géométriques ...
Le billard cosmique
Si l'on se place
dans le vide 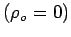 et
que l'on pose
et
que l'on pose
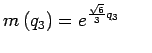 et et
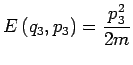 |
(20) |
l'introduction d'un "super-temps"( nom initié par R. Jantzen)
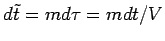 permet d'écrire les équations de la
dynamique de l'Univers sous la forme
permet d'écrire les équations de la
dynamique de l'Univers sous la forme
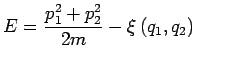 avec avec
![$\displaystyle \left\{
\begin{array}[c]{c}
\dfrac{dq_{1,2}}{d\tilde{t}}=\dfrac...
...\partial q_{1,2}}
=-\dfrac{\partial E}{\partial q_{1,2}}
\end{array}
\right.$](img98.gif) |
(21) |
une sorte
d'énergie potentielle apparaît dans le terme
![\begin{displaymath}\begin{array}[c]{cc}
\xi\left( q_{1},q_{2}\right) = & -n_{1}...
...\sqrt{2}}{2}q_{1}+\frac{\sqrt{6}}{6}q_{2}\right) }
\end{array}\end{displaymath}](img99.gif) |
(22) |
Il s'agit donc d'un système hamiltonien à deux dimensions concernant une particule de masse
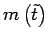 repérée par sa
position
repérée par sa
position
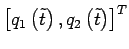 , d'énergie totale
, d'énergie totale
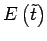 et
dont l'énergie potentielle est
et
dont l'énergie potentielle est
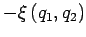 .
La
masse et l'énergie de la particule représentant l'Univers
sont
variables
.
La
masse et l'énergie de la particule représentant l'Univers
sont
variables
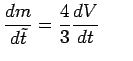 et
et
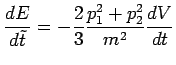
Lorsque l'on se rapproche de la singularité, les
propriétés respectives de 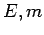 et
et 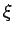 font que la dynamique de
l'Univers homogène et anisotrope sont assimilables à
celles d'une
bille de coordonnées
font que la dynamique de
l'Univers homogène et anisotrope sont assimilables à
celles d'une
bille de coordonnées 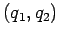 se
déplaçant
dans un billard dont les bandes sont formées par les isovaleurs
de la
fonction
se
déplaçant
dans un billard dont les bandes sont formées par les isovaleurs
de la
fonction 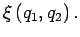 Ces bandes s'éloignent, à
chaque rebond la bille perd un peu de vitesse mais celle ci reste
toujours
supérieure à la vitesse des bandes. Il existe 5 familles
dynamiquement
différentes correspondants aux 5 familles de contours distincts
de la
fonction
Ces bandes s'éloignent, à
chaque rebond la bille perd un peu de vitesse mais celle ci reste
toujours
supérieure à la vitesse des bandes. Il existe 5 familles
dynamiquement
différentes correspondants aux 5 familles de contours distincts
de la
fonction 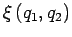 .
.

![$\displaystyle \left\{
\begin{array}[c]{rll}
0 & = & E_{c}+E_{p}+E_{m}\\
\ch...
...^{2}-\left( n_{1}\alpha_{1}-n_{2}
\alpha_{2}\right) ^{2}
\end{array}
\right.$](img70.gif)