
« Dropping a set of beads on a board with evenly distributed pegs results in a binomial distribution. Is it possible to generate other kinds of distributions by varying some parameters ? Is it possible to achieve a distribution that does not obey the central limit theorem in an i.i.d. scenario? What happens to the distribution when one makes the board vibrate? »
La planche de Galton est un dispositif inventé par Sir Francis Galton illustrant la convergence d'une loi binomiale vers une loi normale. On fait tomber des billes à travers un réseau de clous disposés uniformément comme présenté ci-dessous.

Examinons en détail le trajet d'une bille : lorsque la bille tombe sur le premier clou, elle a une chance sur deux de tomber à gauche, et une chance sur deux de tomber à droite. De là, elle peut à nouveau tomber soit à gauche, soit à droite, toujours avec une probabilité \(\frac{1}{2}\), et ainsi de suite jusqu'à tomber dans l'un des compartiments. Formalisons cela.
Soit \(S_n \in \{1,\dots,n\}\) la variable aléatoire représentant le compartiment dans lequel tombera la bille, pour une planche constituée de \(n\) rangées de clous (et donc de \(n+1\) compartiments). Soit \(X_i \sim \mathcal{B}\left(\frac{1}{2}\right)\) une variable aléatoire suivant une loi de Bernoulli de paramètre \(\frac{1}{2}\). \(X_i\) représente la direction de chute de la bille sur le \(i\)-ème clou : \(X_i=0\) (respectivement \(X_i=1\)) si la bille tombe à gauche (respectivement à droite). En numérotant les compartiments de \(0\) à \(n\), où \(n\) est le nombre de rangées de clous, le numéro du compartiment dans lequel tombera la bille s'obtient en sommant les résultats des \(n\) expériences de Bernoulli $$S_n = \sum_{i=1}^n X_i$$ \(S_n\) suit donc une loi Binomiale en tant que somme de variables aléatoires indépendantes de loi de Bernoulli de même paramètre \(p=\frac{1}{2}\). C'est là que le théorème central limite intervient : lorsque \(n\) tend vers l'infini, \(S_n\) tend vers une loi normale en tant que somme de variables aléatoires réelles, indépendantes et identiquement distribuées (i.i.d.) \(S_n \sim \mathcal{N}(\mu,\sigma^2)\) Ce raisonnement repose sur deux hypothèses fortes. Premièrement, les \(n\) expériences de Bernoulli sont supposées indépendantes. Autrement dit, la direction de chute (droite ou gauche) d'une bille sur le clou \(i\) ne dépend pas de la direction de chute de la bille sur le clou \(i-1\). Deuxièmement, on a supposé que la probabilité \(p\) de tomber à droite ou à gauche était constante et égale sur tous les clous : \(p = \frac{1}{2}\). Ces deux hypothèses sont fortes comme nous le verrons dans la suite.
On étudie dans un premier temps l'influence de deux paramètres : la taille des billes et l'inclinaison de la planche de Galton. Nous en construisons donc une pour mener nos expériences. Le dispositif expérimental est présenté ci-après

Une caméra fixée au cadre filme les billes chuter dans les compartiments. Un programme les compte automatiquement.
On commence par tester les performances de notre planche : obtient-on une gaussienne ? Comment quantifier la qualité de la gaussienne obtenue ? On introduit deux grandeurs qui vont nous permettre de répondre à ces questions : la skewness et le kurtosis.
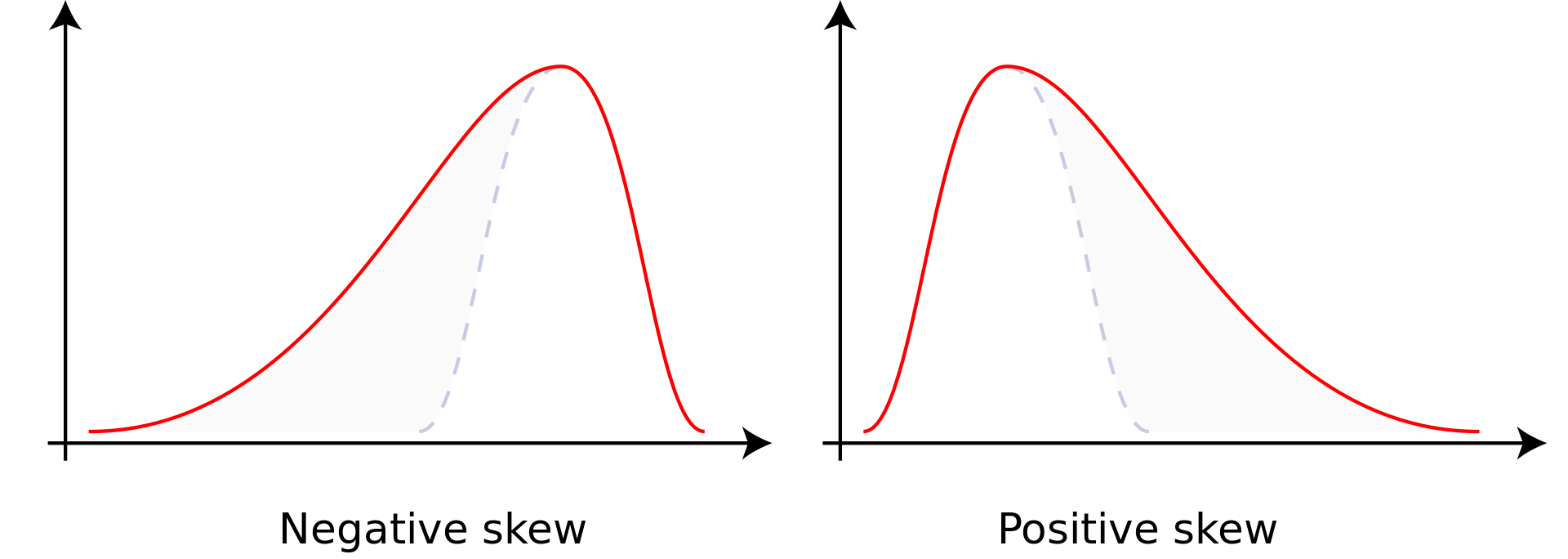
Étant donné une variable aléatoire réelle \(X\) de moyenne \(\mu\) et d'écart-type \(\sigma\), on définit son asymétrie (ou skewness en anglais) \(\gamma_1\) comme son moment d'ordre trois, et son kurtosis non normalisé \(\beta_2\) comme son moment d'ordre quatre. $$\gamma_1 = \mathbb{E}\left[\left(\dfrac{X-\mu}{\sigma}\right)^3\right] \quad \text{et} \quad \beta_2 = \mathbb{E}\left[\left(\dfrac{X-\mu}{\sigma}\right)^4\right]$$ Graphiquement, une asymétrie négative (resp. positive) correspond à une gaussienne penchée vers la droite (resp. penchée vers la gauche ) comme présenté ci-dessous
De même, il existe une typologie pour le kurtosis : si \(\beta_2 = 3\), la distribution est dite mésokurtique. Si \(\beta_2 < 3\), la distribution est dite platykurtique et si \(\beta_2 > 3\), la distribution est dite leptokurtique.
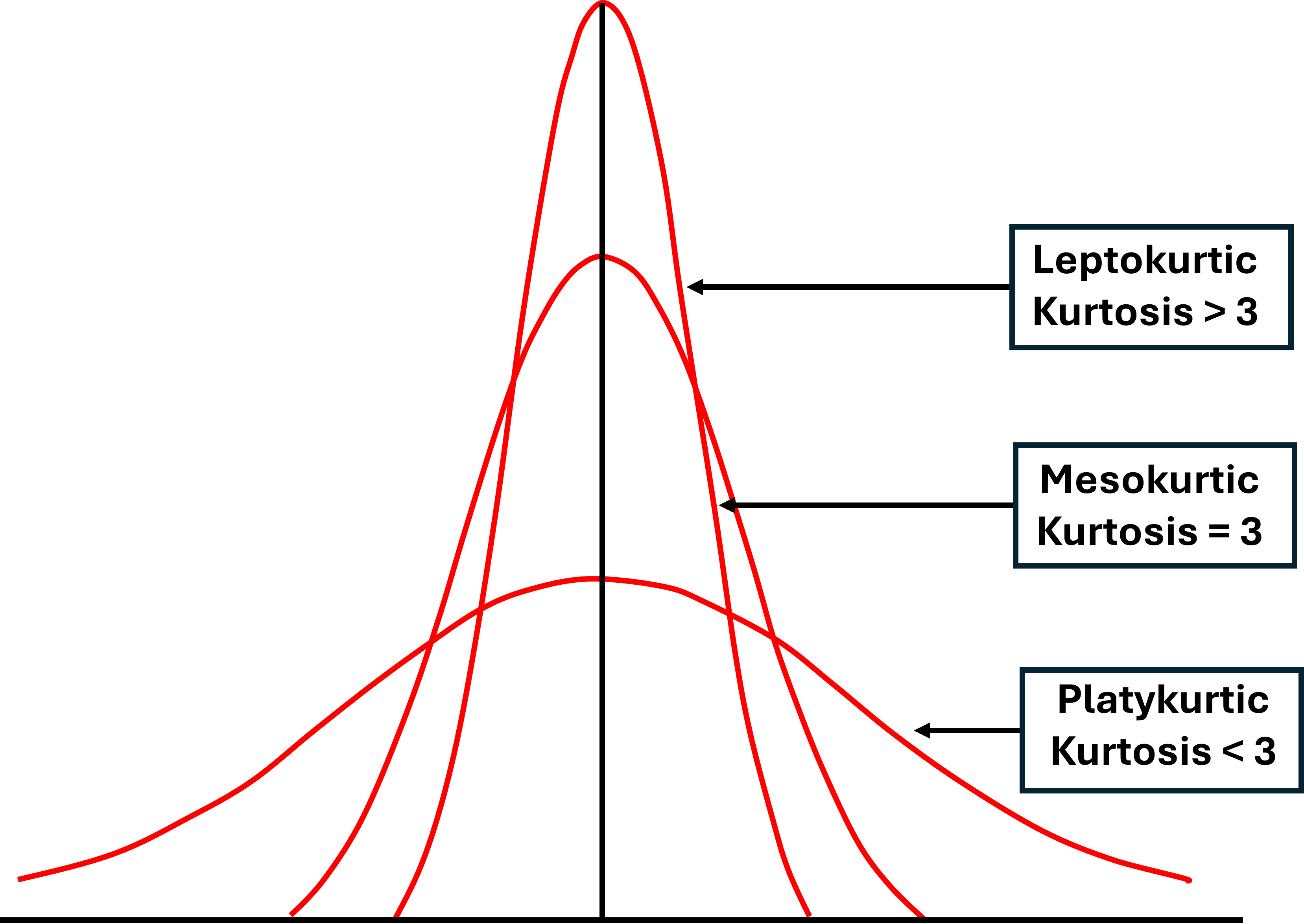
Pour une loi normale, on a une asymétrie \(\gamma_1 = 0\) et un kurtosis non normalisé \(\beta_2 = 3\).
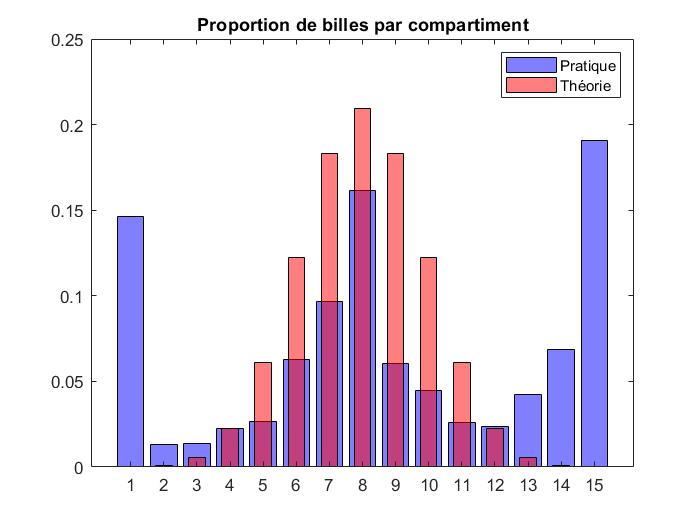
On lâche environ 700 billes dans notre dispositif et l'on compte automatiquement le nombre de billes dans chaque compartiment. On obtient le résultat suivant
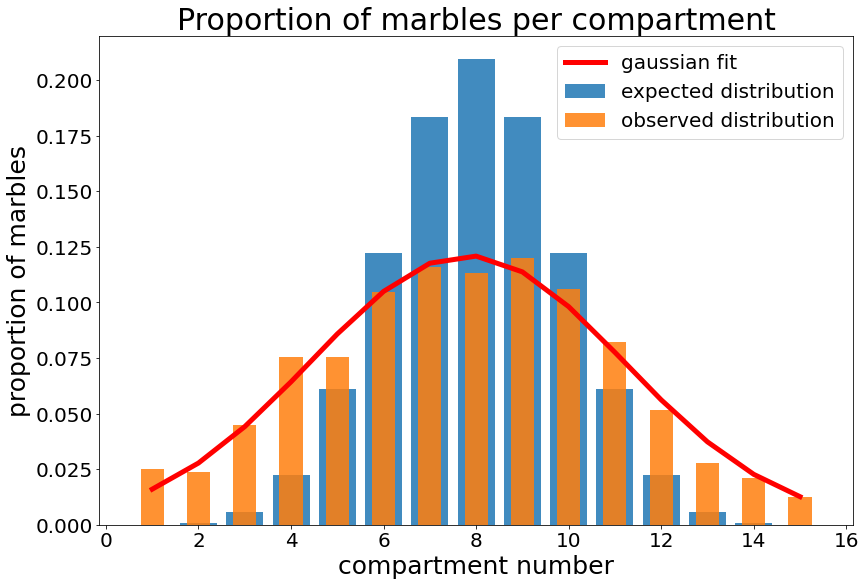
La distribution théorique est obtenue comme suit : pour chaque compartiment \(k \in \{0,\dots,n\}\), on a la proportion de billes suivante : $$\dfrac{1}{2^n}\binom{n}{k}$$ On constate que la gaussienne obtenue expérimentalement est aplatie : la distribution est platykurtique. D'où cela peut-il provenir ? Essentiellement de la non indépendance des variables aléatoires \({(X_i)}_{i\leq 1 \leq n}\) : lorsqu'une bille tombe à gauche au niveau du clou \(i\), elle a plus de chance de tomber à gauche pour le clou \(i+1\) (idem à droite), ce qui aplatit la gaussienne.
On étudie dans cette partie l'influence de l'inclinaison de la planche. Pour ce faire, on calcule la skewness et le kurtosis pour différentes inclinaisons \(\alpha\) de la planche. On obtient les points suivants
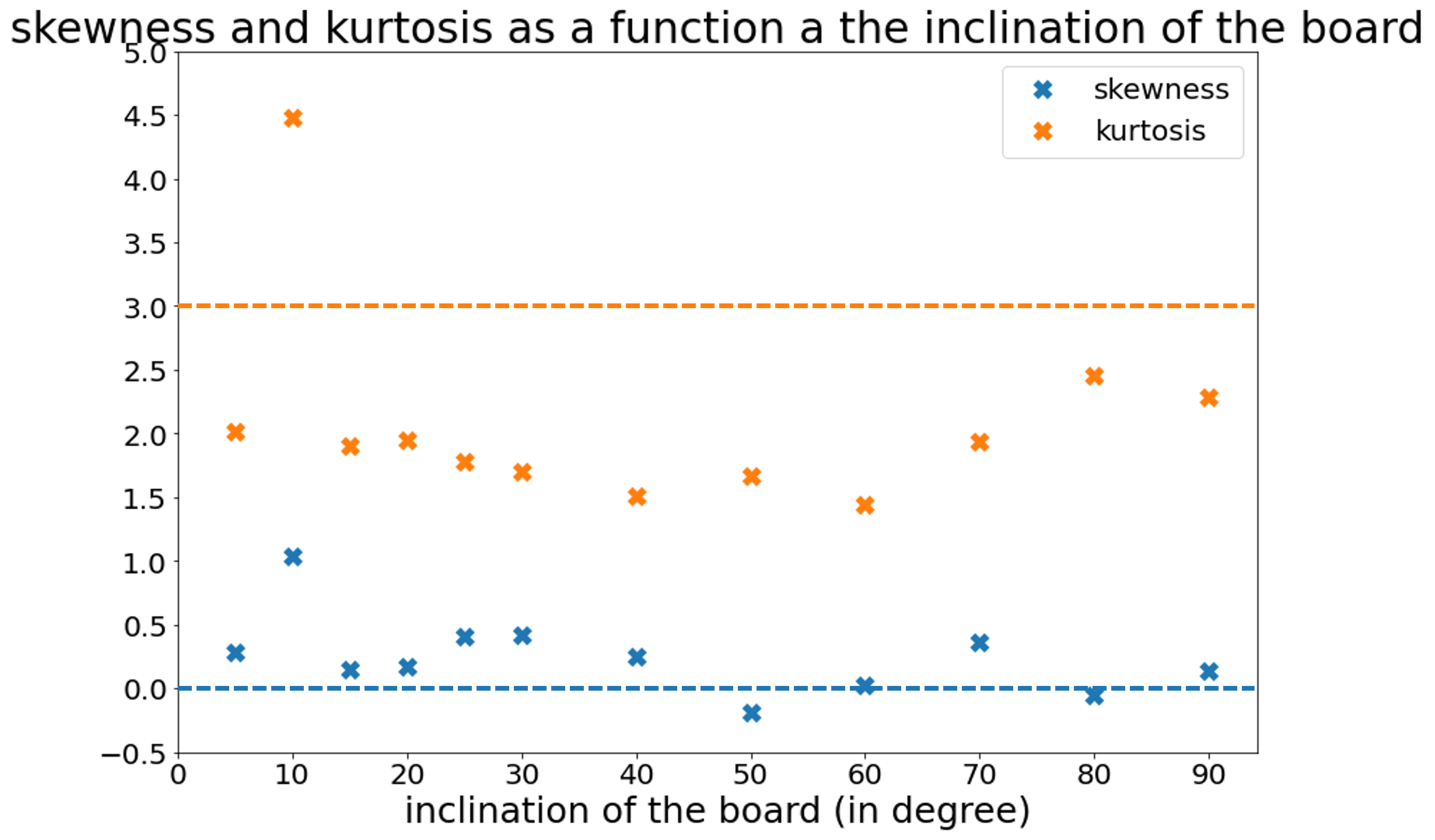
Mis à part une valeur aberrante pour \(\alpha = 10^{\circ}\), le kurtosis est systématiquement inférieur à 3 (autrement dit la distribution est platykurtique), et la skewness oscille autour de 0 : la distribution est globalement symétrique.
On observe en effectuant l'expérience avec des billes de petit diamètre, de diamètre moyen et de gros diamètre, que la taille des billes (ainsi que leur masse) n'a pas d'influence sur la distribution obtenue.
Pour l'instant, on peut conclure qu'en faisant varier la taille des billes et l'inclinaison de notre planche, on ne peut pas obtenir autre chose qu'une distribution gaussienne. Il faut donc faire varier la taille et la disposition des clous. Expérimentalement, il faudrait construire plusieurs planches avec différentes tailles de clous, ce qui est inenvisageable en pratique. On va donc simuler numériquement notre planche de Galton.
On simule numériquement notre planche de Galton (même dimensions et mêmes positions des clous). La vidéo ci-dessous représente un lâcher de billes avec notre programme.
Il est naturel de vouloir valider la simulation numérique : en effectuant les mêmes expériences, obtient-on les mêmes résultats avec la planche expérimentale et la simulation ?
Commençons par les fréquences statistiques dans les compartiments. En lâchant 500 biles numériques, on obtient la courbe suivante
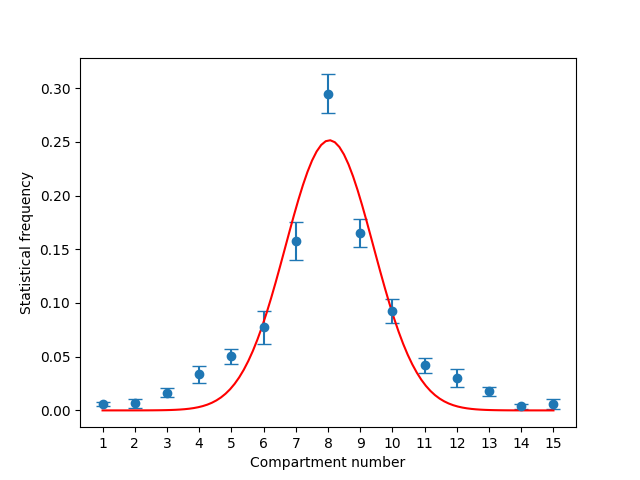
On obtient bien une gaussienne, mais soyons plus précis : étudions le kurtosis et l'asymétrie en fonction de l'angle d'inclinaison de la planche
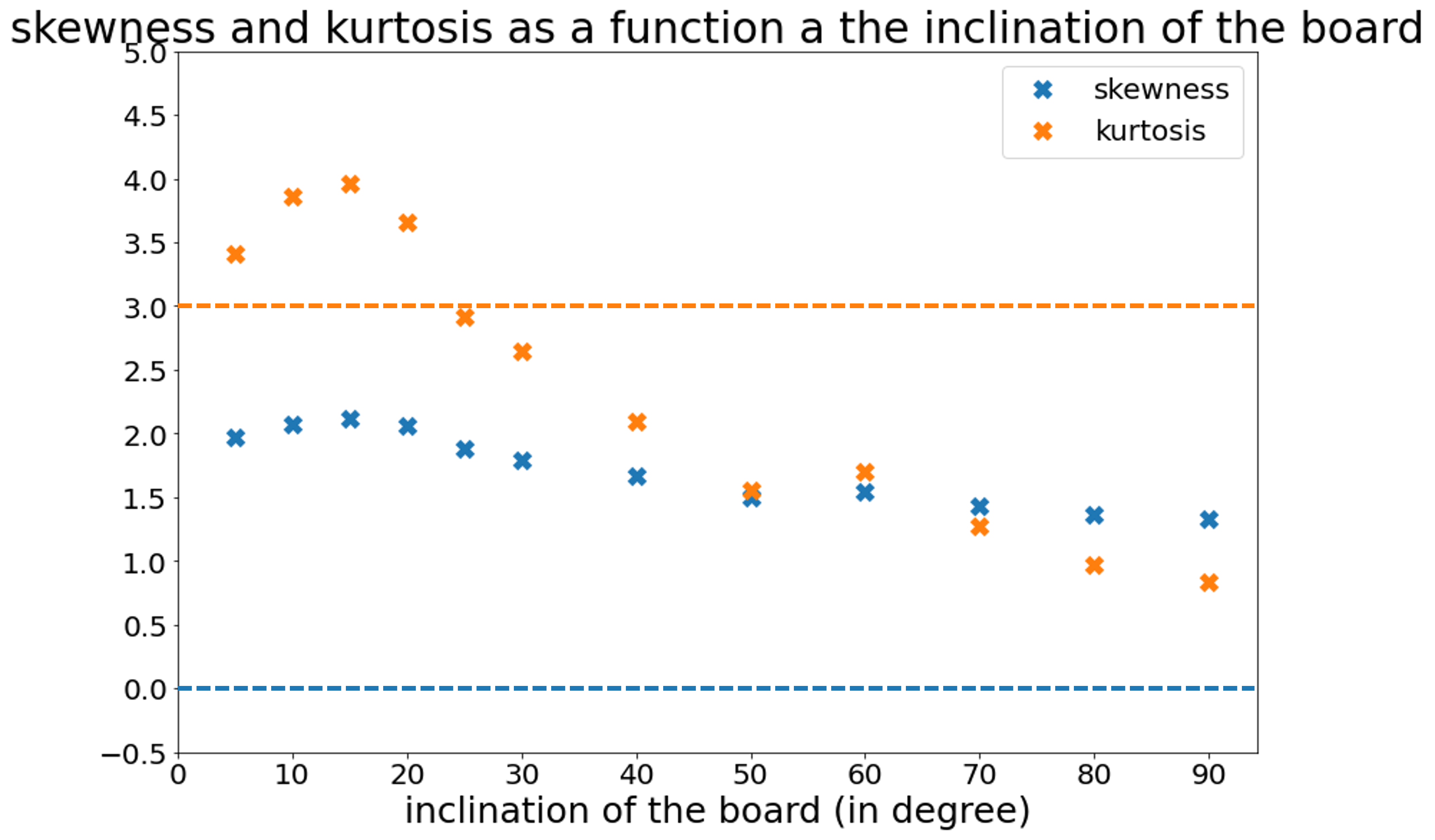
On observe des résultats assez différents qu'avec la vraie planche. Premièrement, le kurtosis peut être soit supérieur soit inférieur à 3 en fonction de l'inclinaison \(\alpha\) de la planche. Autrement dit, en fixant la valeur de \(\alpha\), on peut obtenir une distribution soit leptokurtique, soit mésokurtique, soit platykurtique. Deuxièmement, l'asymétrie est toujours positive, ce qui n'était pas le cas précédemment : la gaussienne est penchée à gauche .
Les résultats expérimentaux et simulés ne coïncident pas. Faut-il jeter la simulation numérique pour autant ? Certainement pas. D'abord parce que l'on n'a que ça, et d'autre part parce qu'elle fournit des résultats précieux. Il est difficile – si ce n'est impossible – de reproduire les résultats obtenus avec notre planche maison : le moindre défaut dans la fabrication de la planche (clou planté de travers, position des clous approximative) peut modifier significativement le résultat final. En réalité, les paramètres choisis (taille des billes, taille des clous, espacement des clous) ne sont pas optimaux pour l'obtention d'une gaussienne normale . Alors comment déterminer ces paramètres ? Avec la simulation numérique ! Cela peut paraître culotté de calculer des paramètres avec une simulation non validée, mais on peut toujours essayer d'obtenir des résultats qualitatifs. Et il faut dire que l'unique alternative, qui consiste à créer moult planches en ne faisant varier qu'un paramètre la fois n'est pas très attrayante...
Toujours à l'aide de notre simulation numérique, on étudie l'influence du rapport du diamètre des billes avec le diamètre des clous. On note dans la suite ce rapport \(\beta\). En particulier, on se demande s'il y a un rapport optimal. On trace pour cela l'asymétrie et le kurtosis en fonction de \(\beta\) et de l'inclinaison \(\alpha\) de la planche.
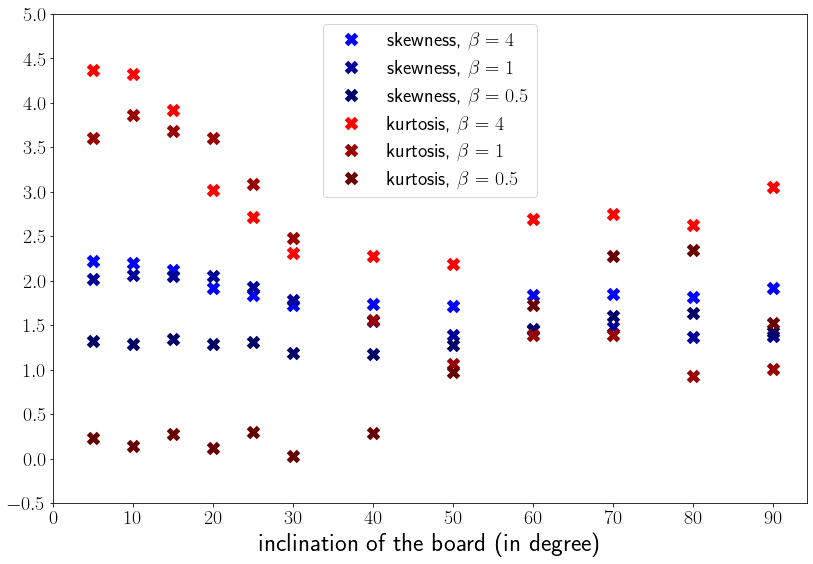
On observe que l'asymétrie diminue lorsque \(\beta\) diminue. Mais cette diminution est relativement faible, ce qui nous pousse à dire que l'asymétrie est à peu près constante égale à 2 et (à peu près) indépendante de \(\alpha\) et de \(\beta\). Pour le kurtosis, c'est tout à fait différent. Pour obtenir un kurtosis \(\approx 3\), on peut soit choisir un \(\beta\) grand (1 à 4) et un \(\beta\) petit (\(20-25^{\circ}\)) soit choisir un \(\beta\) petit (0,5) et un \(\alpha\) grand (\(90^{\circ}\)). Remarquons toutefois qu'il n'y a pas de valeurs de \(\beta\) et \(\alpha\) optimale dans le sens où elles permettraient d'avoir une asymétrie nulle et un kurtosis égal à 3.
Dans l'introduction, une hypothèse forte avait été mentionnée : l'indépendance des \(X_i\), la direction (droite ou gauche) de chute de la bille sur le clou \(i\). En réalité, cette hypothèses peut être plus ou moins vérifiée selon le rapport \(\beta\). Regardons la différence avec la simulation numérique. Commençons par un \(\beta\) élevé
On observe que les billes qui tombent à gauche continuent majoritairement à gauche et idem à droite. En conséquence, il y a des pics de fréquence sur les compartiments extrêmes. On appellera ce phénomène l'effet de bord . En comparaison, changeons à présent la taille des billes
On observe cette fois-ci que ce que l'effet de bord n'intervient plus. Signalons que cet effet n'est pas propre à la simulation numérique. En effet, on l'avait déjà observé avec notre planche expérimentale.
Avec ces nouveaux résultats, on peut conclure que le rapport diamètre des billes sur diamètre des clous (\(\beta\)) joue un rôle important dans la qualité de la gaussienne. Si les billes sont trop petites , le moindre choc avec un clou les envoie traverser toute la planche : la distribution obtenue est platykurtique. Si les billes sont trop grandes , les billes ont tendance à tomber en ligne droite : la distribution obtenue est leptokurtique. D'après notre simulation, il faut des clous de diamètre du même ordre de grandeur que le diamètre des clous. Est-ce la cas dans la réalité ? Une petite expérience nous montre que c'est bien le cas.

La simulation est donc fidèle a la réalité, tant dans la prédiction de phénomènes que dans le calcul des diamètre des billes et des clous. La simulation numérique est donc bien validée. Revenons donc à notre problème : comment disposer les clous de sorte à obtenir une distribution non binomiale ? On commence avec une méthode simple pour obtenir une distribution quelconque : la méthode des quantiles.
Le principe de cette méthode est simple : on place les clous au niveau des quantiles de la distribution souhaité comme décrit par la figure suivante
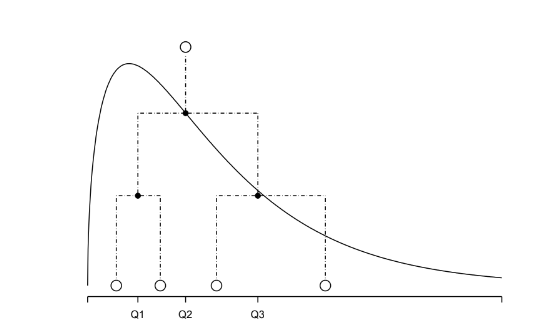
Les ordonnées des clous sont calculées de sorte que les billes qui viennent de rebondir sur un clou de la rangée \(n\) tombent sur un clou de la rangée \(n+1\). En pratique, pour une loi du Khi-deux de paramètre \(k = 4\), que l'on notera \(\chi^2_4\) dans la suite, la disposition de clous est la suivante
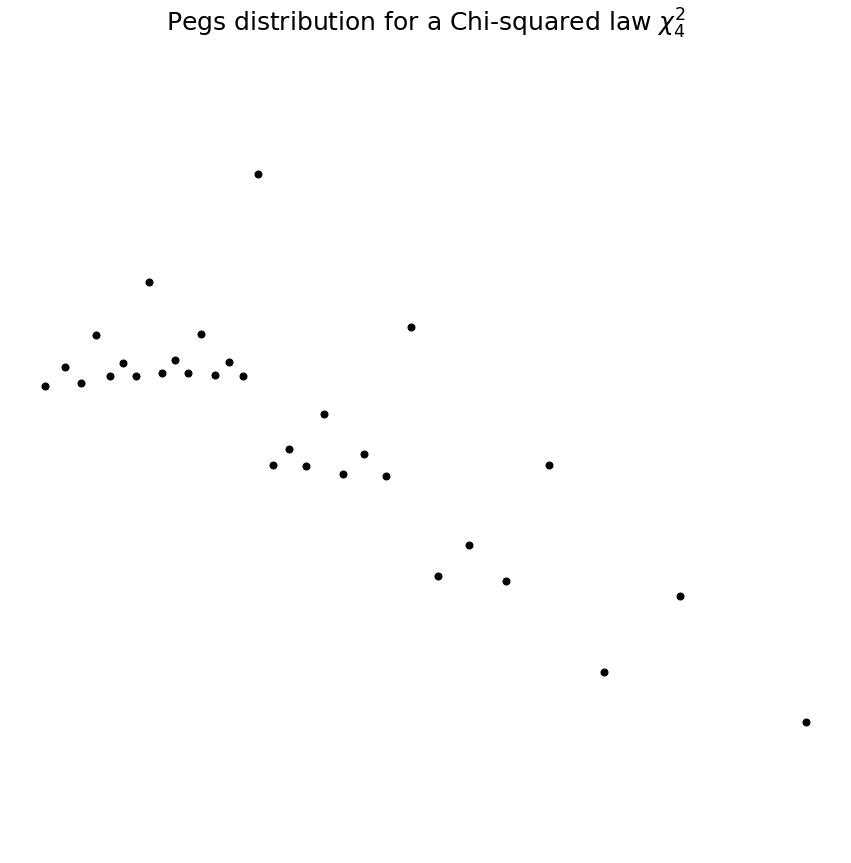
On obtient alors les fréquences statistiques suivantes
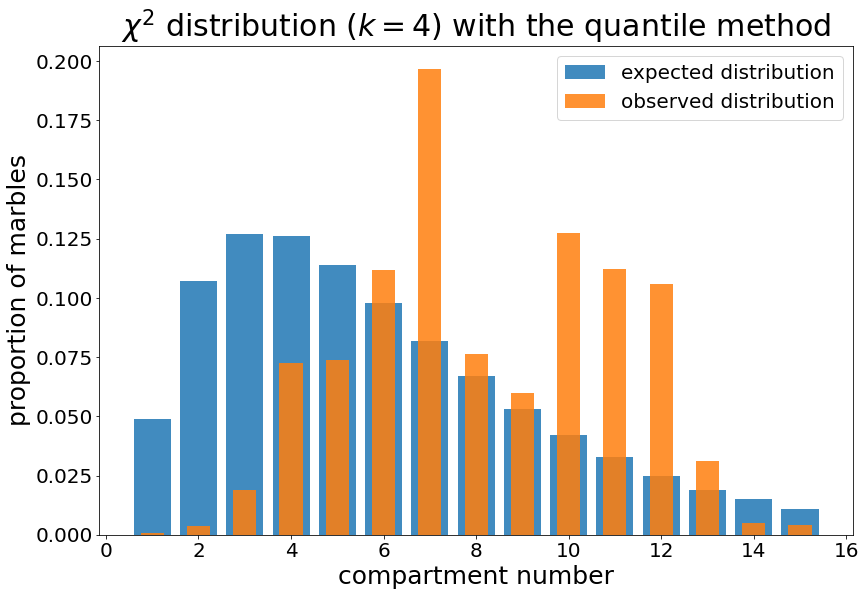
Bonne nouvelle : on a réussi à produire une distribution non binomiale. Mauvaise nouvelle : ce n'est pas vraiment la distribution attendue. Cela est dû à deux facteurs. Premièrement, les billes tombent fréquemment d'une rangée \(n\) à une rangée \(n+d\) où \(d > 1\), et deuxièmement, certains clous sont trop proches et les billes se coincent dedans. On essaye donc une méthode radicalement différente, qui s'appuie sur du machine learning.
Comme précédemment, le principe de la méthode est simple : on génère des positions de clous aléatoires, et on observe lesquelles permettent au mieux de générer une distribution du Khi deux. On fait ensuite de petites variations sur ces positions de clous pour essayer de peaufiner. On obtient par exemple les dispositions de clous suivantes

avec les fréquences statistiques suivantes
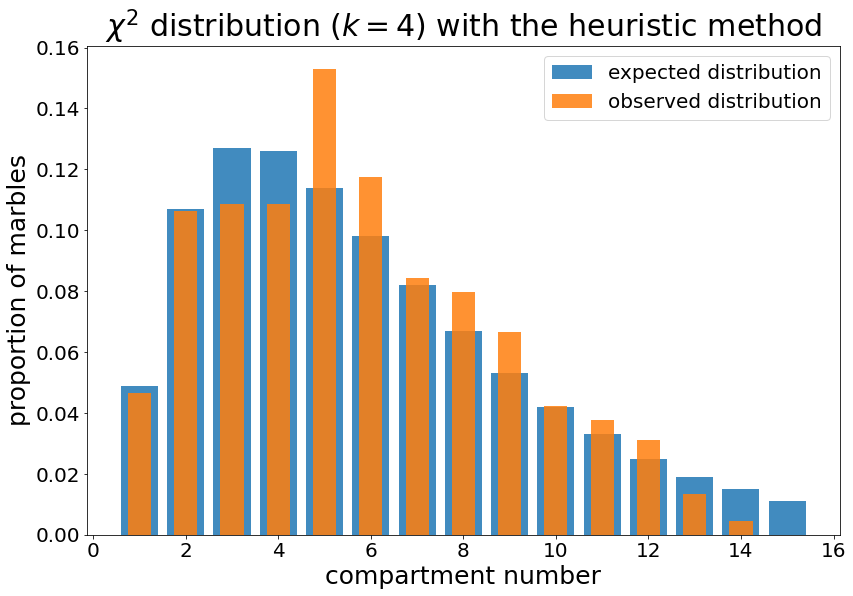
Un résultat bien plus convaincant, qui a le défaut d'être long à calculer (quelques heures). Avec cette approche, on peut aisément trouver une disposition de clous permettant d'obtenir n'importe quelle distribution.
“GALTON BOARD” in Chaotic dynamics V. V.KOZLO and M.Yu.MITROFANOVA,
2005
Beyond the Quintessential Quincunx, Michael A. Proschan and Jeffrey S.
Rosenthal