I - Introduction
In this study, we examine the behavior of a flag, or more generally a sheet of material, when subjected to uniform wind, and seek to understand the conditions under which it begins to flap and how the flapping sound relates to the wind speed.
It is essential to consider the material of the flag in this analysis, as its air-transmitting capacity will affect the behavior of the air flow surrounding the flag and thus influence its flapping behavior.
To ensure controlled conditions, we chose a plastic sheet that does not permit any air to pass through.
Furthermore, we hung the flag vertically, neglecting the impact of gravity on its behavior, which would need to be considered if it were hung horizontally.
We also introduce several important parameters for this problem:
| Parameters |
| Dimensions | Mass | Young's modulus |
| Lenght L | Linear density m | E |
| Height H | Density ρ | |
| Thickness e | |
II - Theory
The equation that governs the flag's behavior is derived from the Euler-Bernoulli beam theory, where the stiffness of the material represents the flag's resistance to the imposed air pressure.
Our hypothesis assumes that the flag does not permit any air to pass through, which assures that the pressure between the two faces of the flag is in agreement with the theorem.
III - Experimental
To accurately measure the flag's behavior, specifically the sound it produces when subjected to a constant airflow, we replaced our plastic sheet in an Eiffel wind tunnel.
This allowed us to fix the speed of the airflow while maintaining silence so that we could measure the sounds produced by the flag.
It is crucial to note that we attached the flag as thinly as possible to minimize the influence on the initial interaction between the flag and airflow, avoiding any significant attachments or obstacles that could affect the flag's behavior.
We used a microphone to record the sounds and filtered the recordings to eliminate any extraneous noise.
IV - Start of Flapping
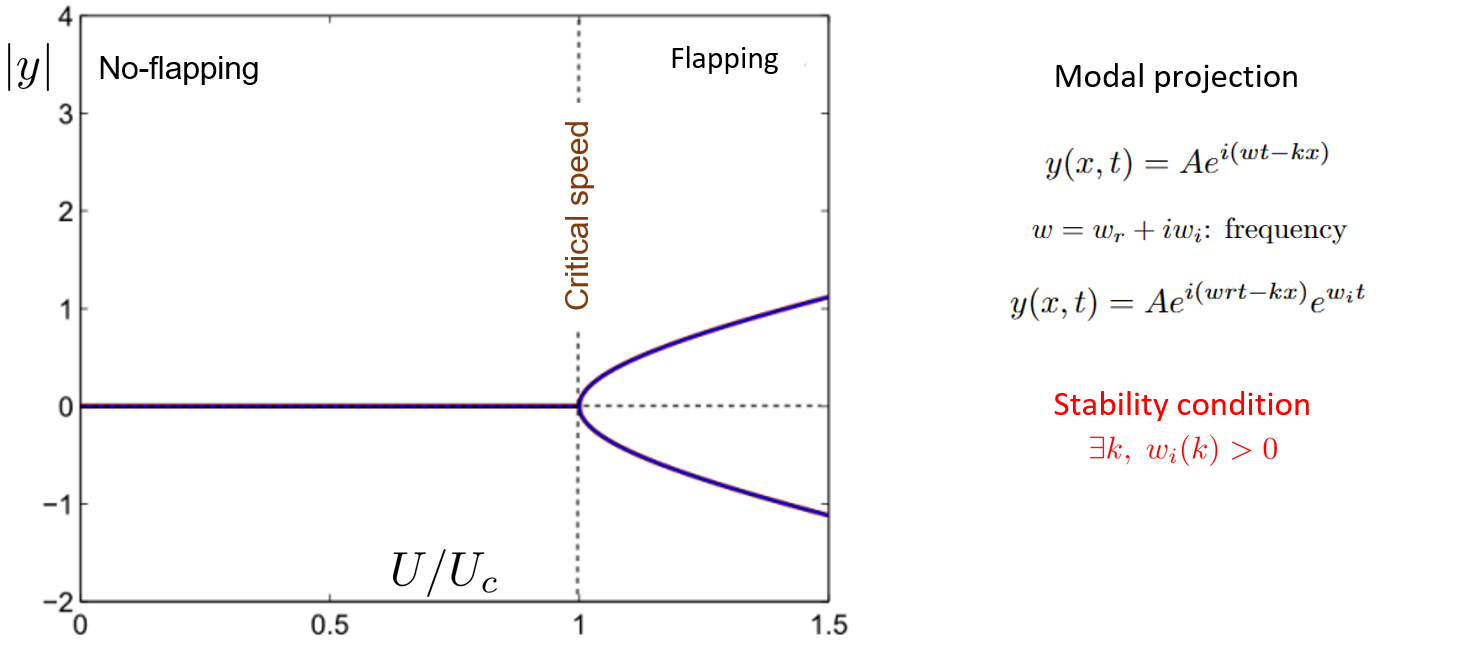
Using our theoretical analysis, we can comprehend the phenomenon of the flag's start of flapping, which is the critical wind speed at which we can observe its flapping behavior.
To find solutions to our equation, we used modal projections that employ a complex frequency. As soon as the imaginary part of this complex frequency becomes positive, flapping is observed.
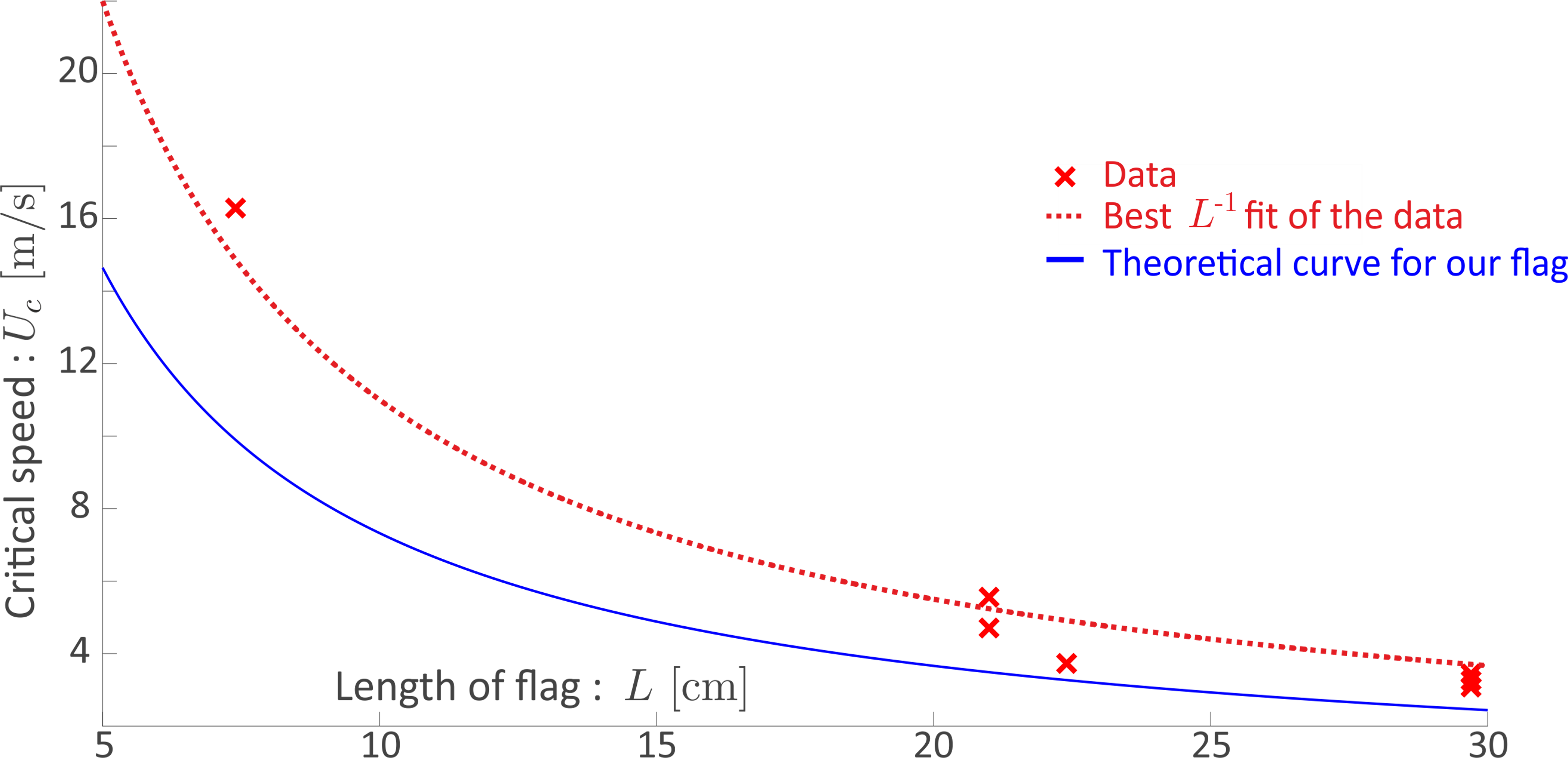
By measuring the different critical wind speeds for various flag lengths, we can compare the behavior of our flag to the theoretical behavior and ascertain the validity of our theoretical model.
V - Anemometer
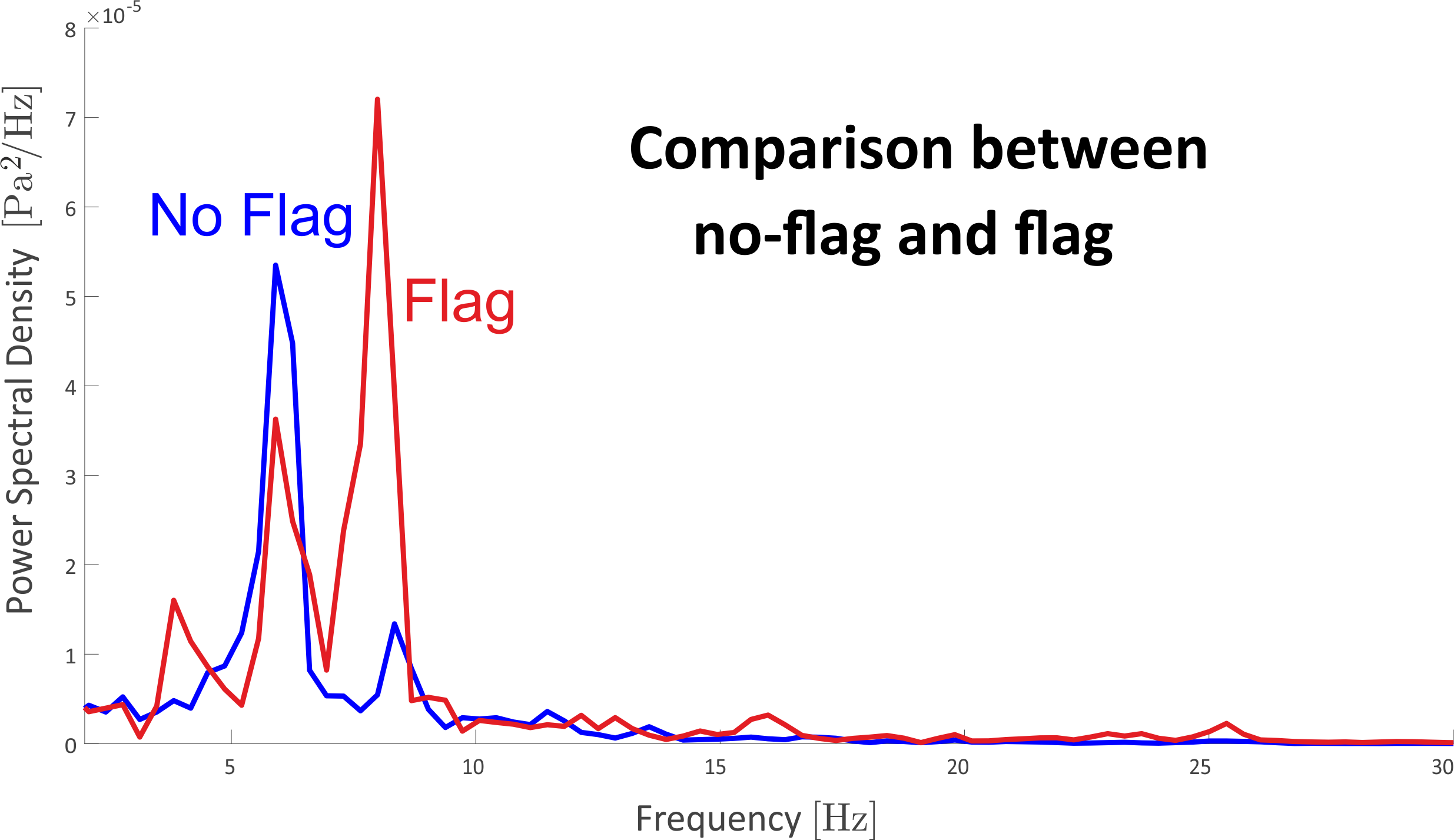
To identify the flapping frequency, we record the sound inside the wind tunnel with and without the flag in it.
Now, we know where to look to find the flapping frequency.
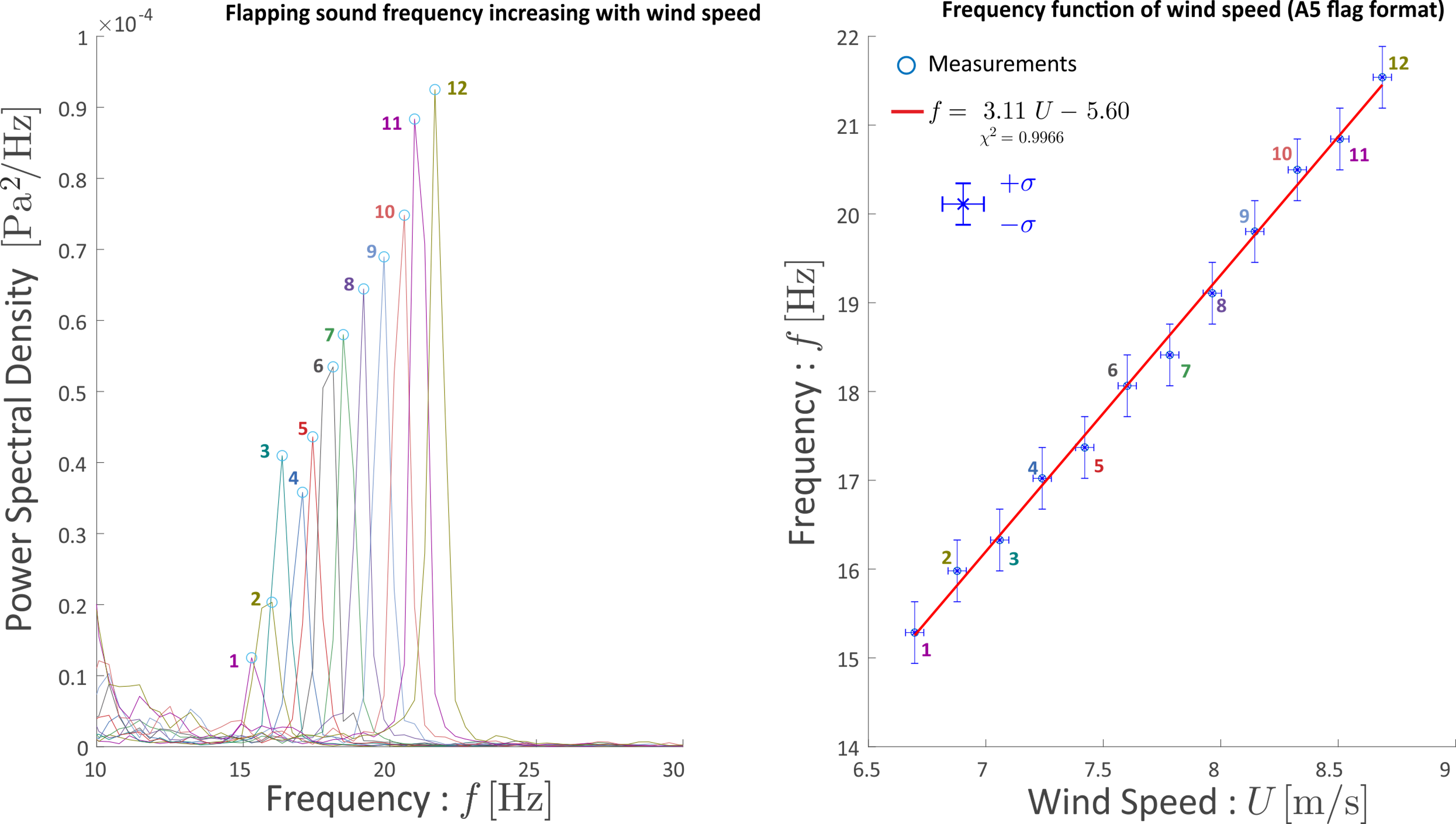
In order to construct an anemometer using a flag, we must calibrate it.
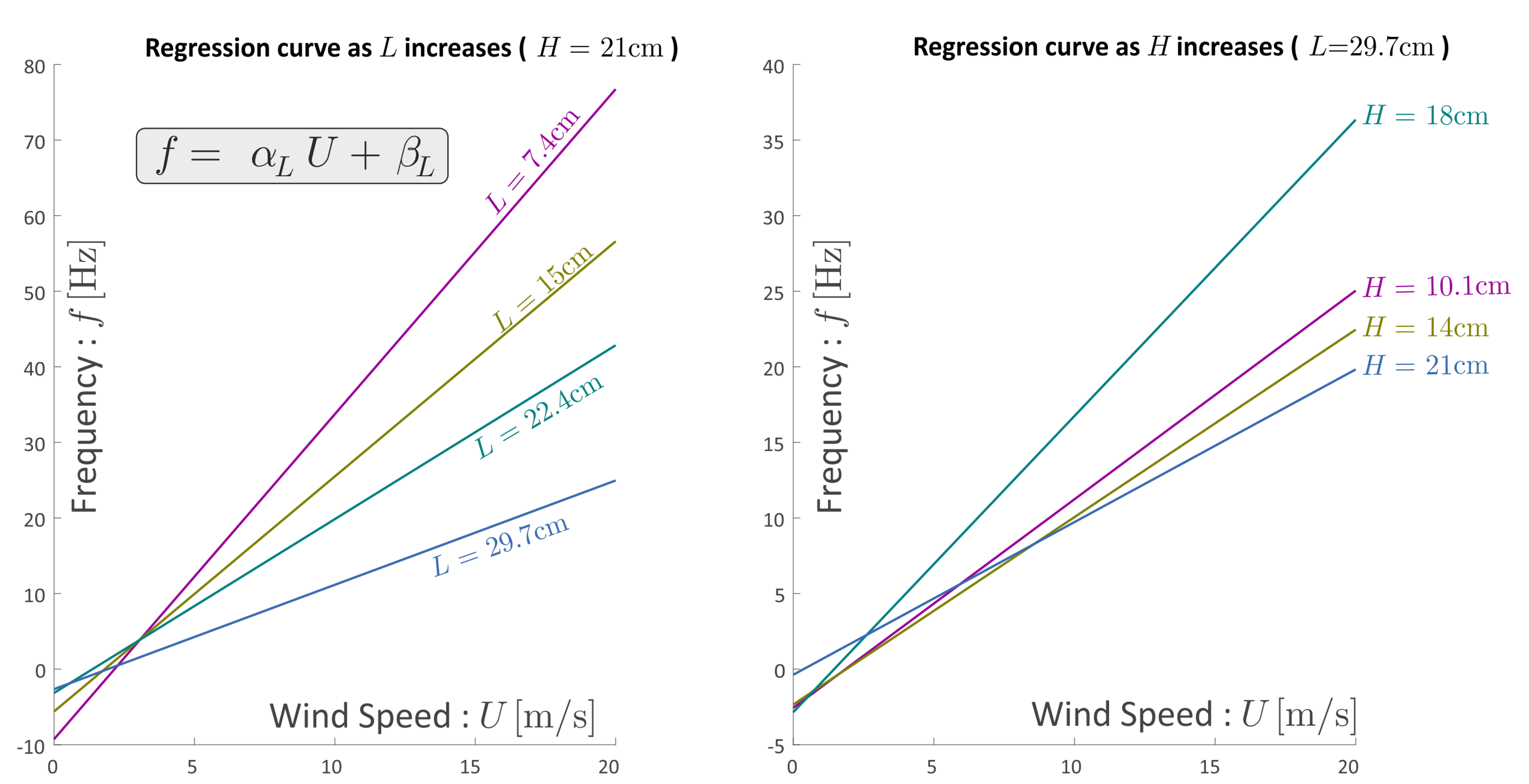
To do so, we measured the flapping frequency as the wind speed increased, as shown in the graph.
These results indicate that one can build an anemometer using a flag for reasonable air flow speeds.
VI - Anemometer without Calibration?
Can we build an anemometer without calibrating it, knowing only the characteristics of the flag, such as its length, height, density, or Young's modulus?
To investigate, we examined the effect of varying each of these parameters on the flag's behavior.
We found that the frequency varies with the length but is independent of the flag's height.
Therefore, once a flag is calibrated for a particular length, an anemometer can be constructed for flags with the same characteristics but different lengths.
VII - Conclusion
In conclusion, we have demonstrated that an anemometer can be constructed using only a flag, and our study provides a method for calibrating it for reasonable wind speeds.
However, it is important to note that the calibration may not be valid for higher wind speeds due to the emergence of different frequencies.
Nevertheless, our study contributes to the understanding of flag behavior in uniform wind and its potential use as an experimental measuring tool.
Bibliography
[1] Flutter of cantilevered plates in axial flow, L. Huang, Peterhouse, University of Cambridge, 1994
[2] Flutter of a rectangular plate, C. Eloy, C. Souilliez, L.Schouveiler, IRPHE, CNRS, Universités Aix-Marseille, 2007
[3] Flottement de drapeau : dynamique et couplage, E. Virot. Mécanique [physics.med-ph]. Ecole Polytechnique, 2015. Français. fftel-01162549v2ff