Coffee Cup Project


Prenez une tasse à café ou un mug. Ce sont des objets communs que l’on possède tous chez soi. Prenez ensuite une cuillère, c’est encore une fois un objet relativement commun, que l’on possède chez soi. Essayez de plonger la cuillère dans votre tasse ou votre mug vide et de taper aux 3 quarts de la hauteur de l’objet. Vous entendez que la tasse émet un son, plus ou moins important et plus ou moins aigu en fonction du matériaux de votre tasse ou de votre mug. Essayez maintenant de taper sur la tasse toujours à la même hauteur mais en vous déplaçant le long du périmètre du cercle de votre objet. Vous pourrez observer, si vous tendez l’oreille, que la hauteur du son, c'est-à-dire si la note est plus ou moins aiguë, change en fonction de là où on tape. On peut même remarquer que le son change de façon périodique par rapport à l’angle entre le point d’impact et le centre de l’anse de la tasse ou du mug. Le son émis dépend fortement du point d’impact
On peut continuer à étudier notre objet de la sorte. Faire des enregistrements, construire un modèle, et ainsi de suite … De nombreux scientifiques se sont déjà penchés sur la question et on peut facilement obtenir à partir de la connaissance de l’objet et la connaissance de l’endroit d’impact. Cette question bien que très intéressante et se présentant comme un exercice scientifique intéressant est déjà résolue. Dans notre étude nous ne sommes pas intéressés à l’étude de ce problème direct. C’est-à-dire, prédire le spectre fréquentiel du son produit en tapant sur différentes parties de la tasse. Nous avons cherché à retrouver la forme de la tasse (ou plutôt des informations sur la forme de la tasse) à partir des sons qu’elle émet lorsqu’on tape dessus. En résumé, notre problème consiste à: mettre en place une méthode expérimentale pour retrouver la forme de la tasse à partir du son qu’elle produit. On se posera donc la question de savoir : quelle est la quantité minimale d’informations sur sa géométrie pour rendre ce problème soluble ?
La première idée que nous avons eu a été d’enregistrer les sons issus des vibrations des tasses que l’on considérait, d’en déduire les fréquences de résonance de la tasse plus de remonter aux caractéristiques de la tasse. La logique derrière ce raisonnement était de considérer notre tasse comme un objet vibrant et ayant des modes de vibration, conformément à la théorie des systèmes dynamiques. Nous modélisons, ici, notre tasse comme une demie coque sphérique creuse. Cet objet possède donc des modes de vibration qu’il nous faut retrouver. Une fois que nous avons identifié ces modes on peut utiliser les équations du modèle des systèmes dynamiques (modèle bien connu des scientifiques modernes, comme nous l’expliquions plus haut) en générant un grand nombre de modes propres relatif à des tasses ayant des caractéristiques connues puis en comparant les différents modes propres générés avec ceux de notre tasse on retrouve les caractéristiques de notre tasse.
Afin de faire cela il nous fallait donc faire deux choses. D’une part, obtenir les modes propres de notre tasse. Pour cela il fallait enregistrer le son émis par la tasse lorsqu’on la tape puis analyser le signal. D’autre part, il nous fallait générer des modes propres pour plusieurs valeurs des paramètres de la tasse et comparer la base de données générée avec les valeurs acquises lors de l’expérience
Le montage expérimental est composé de plusieurs éléments. La tasse que l’on considère qui était dans notre cas un bécher sans anse par mesure de simplicité mais aussi pour pouvoir jouer sur les paramètre physique de l’objet sans changer le matériaux), la table en marbre sur laquelle était fixé le bécher, un marteau d’impact, un micro ultra directionnel, un ordinateur ainsi que les appareils pour convertir et acheminer les signaux à l'ordinateur. Le montage est le suivant :
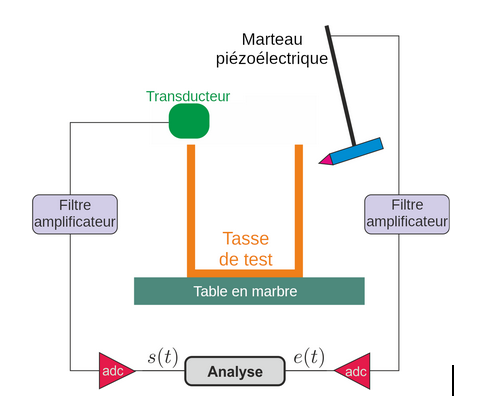
Ainsi le montage permet d’acquérir un signal d’entrée (celui du marteau) et un signal de sortie (celui du micro). On peut ainsi étudier la fonction de transfère de notre signal et s’affranchir des modifications dû au changement de force du marteau : en d’autres termes on connaît précisément la force que l’on met dans l’impact à chaque fois.
Remarque : On peut étudier la fonction de transfert du signal car la réponse de la tasse est linéaire (cf courbes plus tard). Sinon ça n’aurait pas de sens de considérer cette fonctione de transfert.




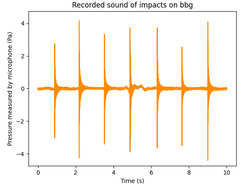
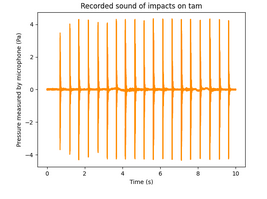
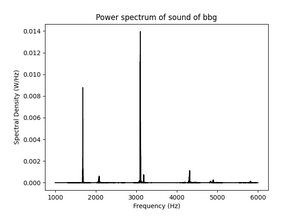
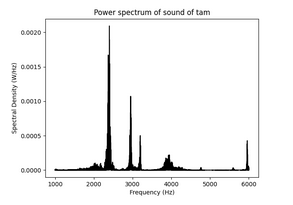
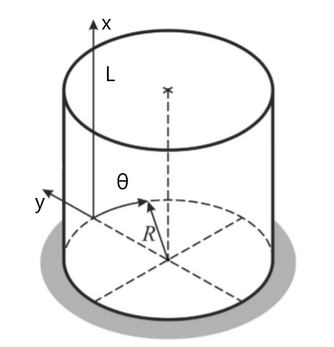
On commence par modéliser une tasse sans anse (bécher) par une coque cylindrique homogène à paroi mince de rayon R, de longueur L, d'épaisseur h, dont la surface centrale est rapportée au repère de coordonnées curvilignes (x,θ).
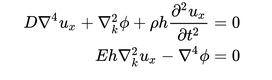
Ces équations permettent de calculer les modes propres et surtout les fréquences propres de vibration :
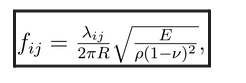
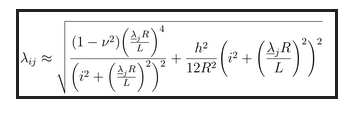

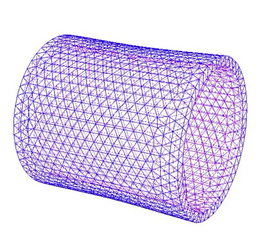
Dans cette partie on étudie la vibration de la membrane de la tasse à l’aide de GMSH (pour générer un maillage de la tasse) et de Freefem++ (solveur d’EDP) en l’automatisant pour tester plusieurs valeurs de R, L et h.
Les équations résolues par Freefem++ pour déterminer les modes propres de vibration du cylindre sont basées sur les lois de l’élasticité suivantes en tenant compte des conditions aux limites:
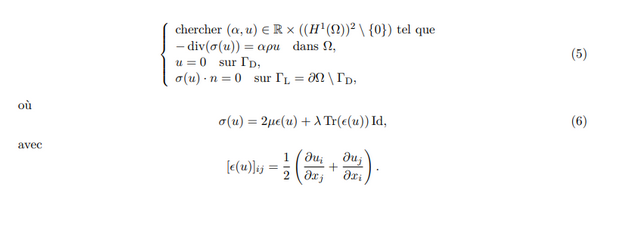

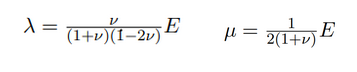
En utilisant la simulation, on peut revenir à R et L aussi précisément qu’avec les résultats analytiques, ici on ne se concentre que sur h.
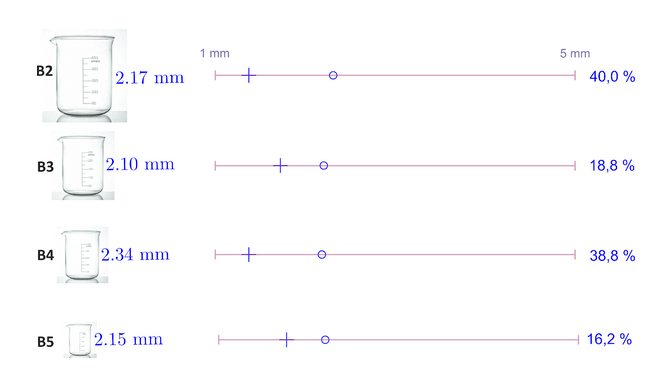
Sur cette figure, on considère 4 béchers de taille différente et on varie l’épaisseur h de 1 à 5 mm, après on génère à l’aide de Freefem++ pour chaque h le spectre de fréquences propres associés et on essaye de le matcher avec les fréquences expérimentales comme à la méthode précédente. Ensuite, on calcule l’écart pour chaque configuration (en pourcentage) entre l’épaisseur exacte et l’épaisseur généré par Freefem++. Le résultat semble satisfaisant pour le bécher le plus petit et donc cette méthode pourrait être une alternative de la première dans le cas où la tasse est assez petite ce qui viole les hypothèses du modèle de la coque cylindrique mince.
Bien qu’on a pas des formules prêtes et des données suffisantes pour traiter ce cas, on s’est restreint au problème de la présence de l’anse ou pas.
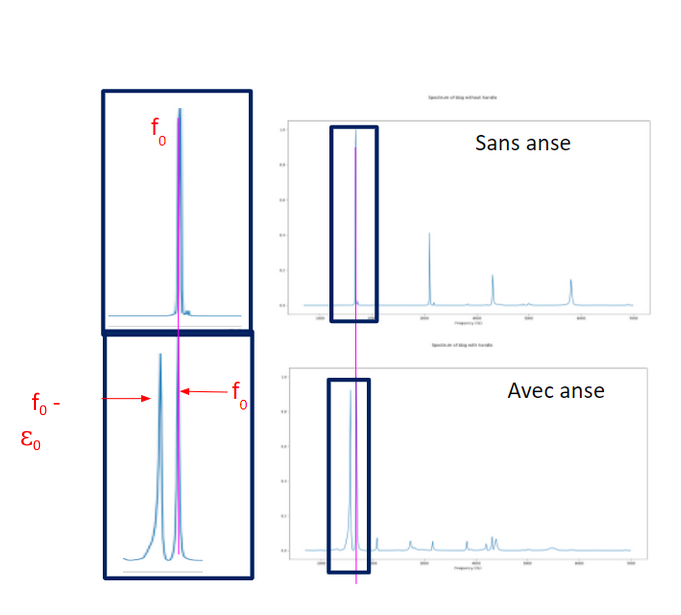
Dans le cas de la présence de l’anse, on constate qu’elle joue le rôle “Tuned mass damper”, qui est un dispositif monté dans les structures (populaire dans les tours) pour réduire les vibrations mécaniques, constitué d'une masse montée sur un ou plusieurs ressorts amortis.
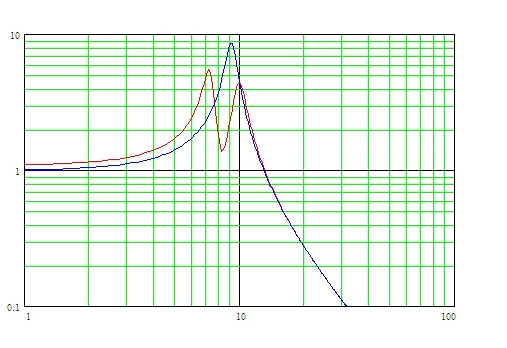
Ainsi ce phénomène nous permet de donner une condition suffisante pour détecter l’absence de l’anse comme vous pouvez le voir ci-dessous.