
Lorsqu'un récipient contenant un matériau granulaire (par exemple du sable) est secoué de manière appropriée, un objet placé au fond remontera à travers le milieu granulaire jusqu'à faire surface. Expliquer le phénomène et déterminer la méthode d'agitation la plus effiace énergétiquement pour faire remonter l'objet.
.
Le phénomène a été particulièrement observé lors du transport de noix dans des camions au Brésil. Ceux-ci roulaient sur des chemins accidentés, ce qui secouait la cargaison. A l'arrivée, les noix les plus grosses se trouvaient au-dessus des autres. Le phénomène est ainsi surnommé "effet noix du Brésil".
Au sein d'un milieu granulaire, principalement deux phénomènes physiques entrent en compétition et peuvent expliquer l'effet noix du Brésil.
Comme présenté sur le schéma ci-dessous, une première explication du phénomène est que la sphère remonte à chaque secousse. Elle laisse ainsi suffisament d'espace en dessous d'elle pour que les grains s'écoulent par avalanche. Les grains s'accumulent dans l'espace libéré ainsi jusqu'à ce que la sphère arrive en surface.
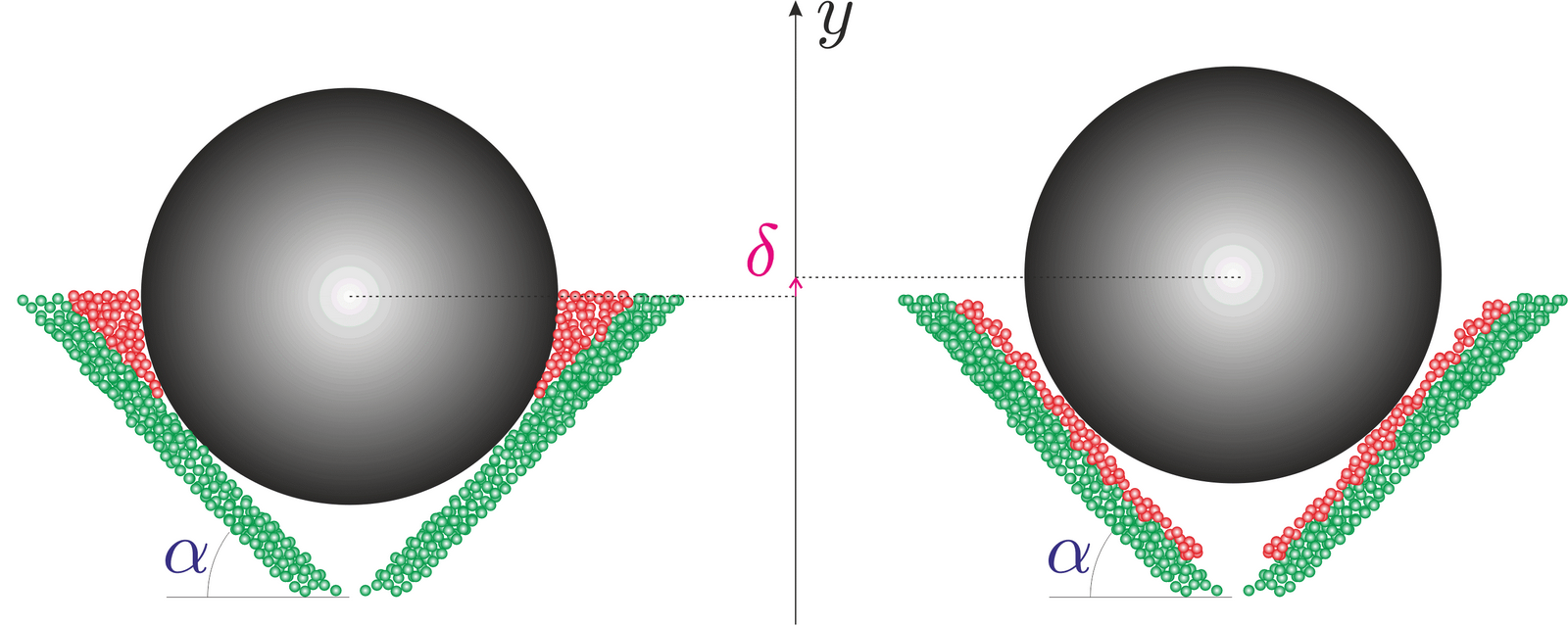
L'autre phénomène possible est la formation de cellules de convection au sein du milieu granulaire. La sphère remonte donc lorsqu'elle arrive au niveau de la branche ascendante de la cellule de convection. Une fois en surface, la sphère peut redescendre ou rester bloquée si la branche descendante est petite devant le diamètre de la sphère.
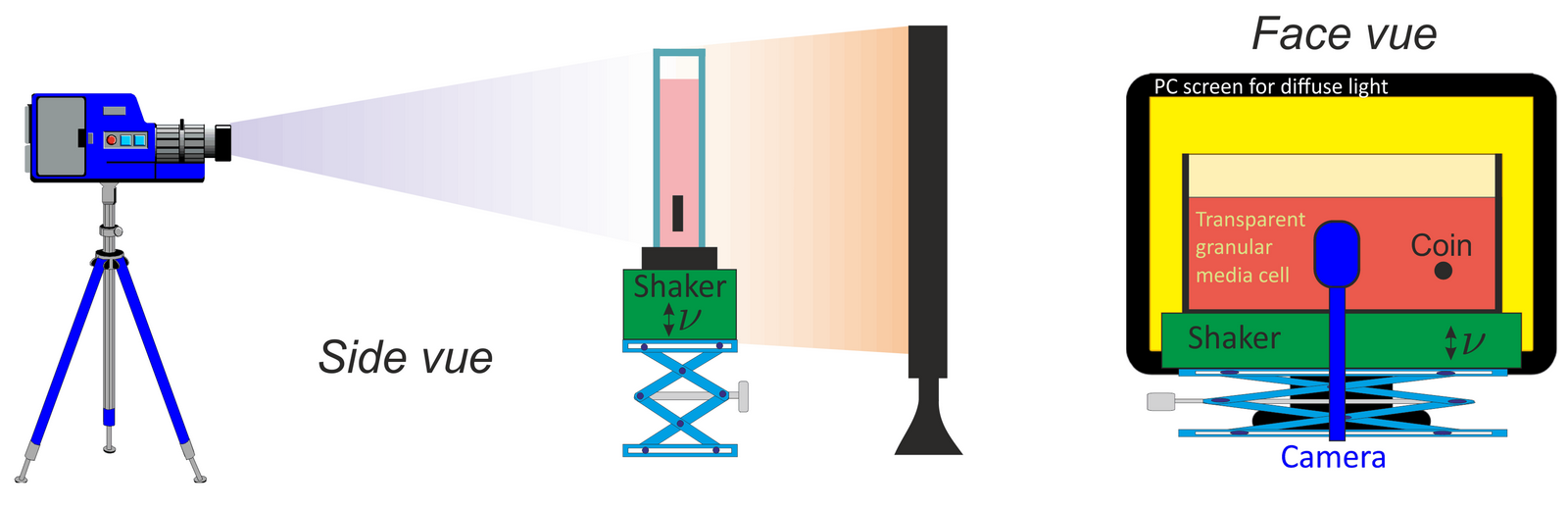
Pour observer et analyser l'effet noix du Brésil, le milieu granulaire transparent (billes de verre ou de plastique) est contenu dans une cellule de faible épaisseur pour observer le phénomène en 2D. Un pot vibrant relié à un générateur basse fréquence permet de secouer le milieu granulaire dans lequel un objet a été placé. L'acquisition se fait à l'aide d'une caméra qui prend les images à une fréquence que l'on peut régler pour qu'elle soit égale à celle du pot vibrant. Un écran diffuse de la lumière derrière la cellule afin d'obtenir un meilleur contraste.
Le montage est présenté sur le schéma ci-dessous :
Les images sont redimensionnées et binarisées pour suivre les objets connexes d'une taille minimale. On peut suivre alors l'objet au cours du mouvement et ainsi obtenir la position et la vitesse comme dérivée de la position en fonction du temps. La reproduction de l'expérience environ une centaine de fois permet d'observer une tendance pour le phénomène.
Les expériences sont effectuées pour des fréquences entre 20 Hz et 35 Hz pour différentes amplitudes. A cette fréquence, une vue rapprochée sur l'objet permet d'observer que le milieu granulaire entoure complètement l'objet et laisse très peu d'espace en dessous de lui à chaque secousse.
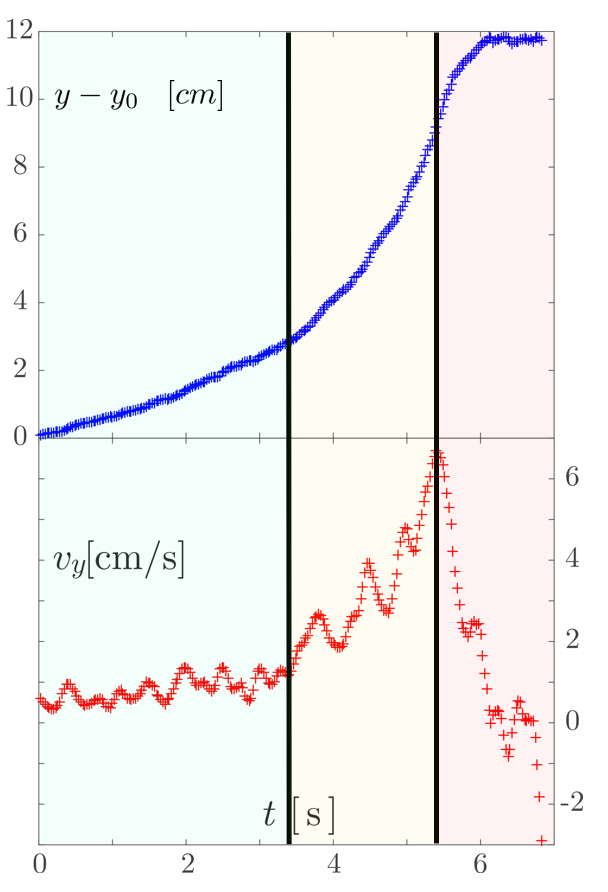
A priori, pour cete gamme de fréquence, la convection est le phénomène dominant à l'origine de la remontée de l'objet dans le milieu granulaire. Trois phases se distinguent sur la courbe représentant la position verticale (axe Oy) et la vitesse verticale en fonction du temps : une phase de mise en mouvement pendant laquelle l'objet se place au niveau de la branche ascendante de la convection, une phase d'accélération pendant la remontée, puis une phase proche de la surface où l'objet ralentit très fortement avant de rester en surface.
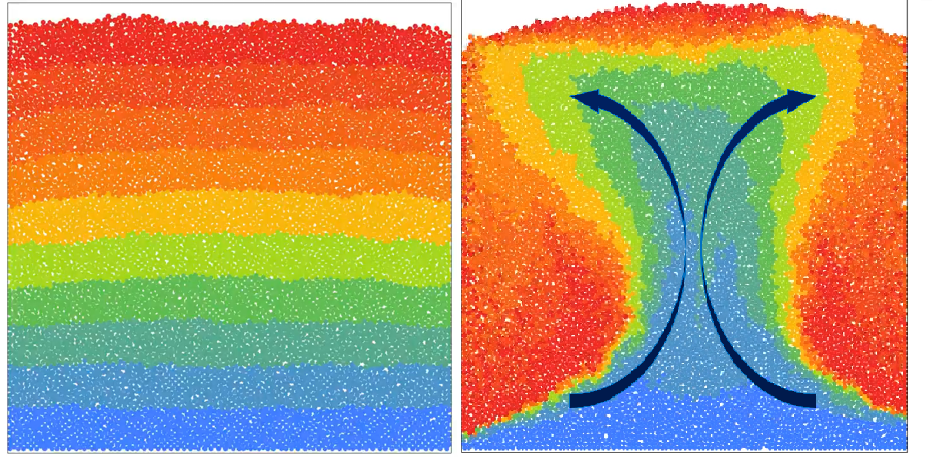
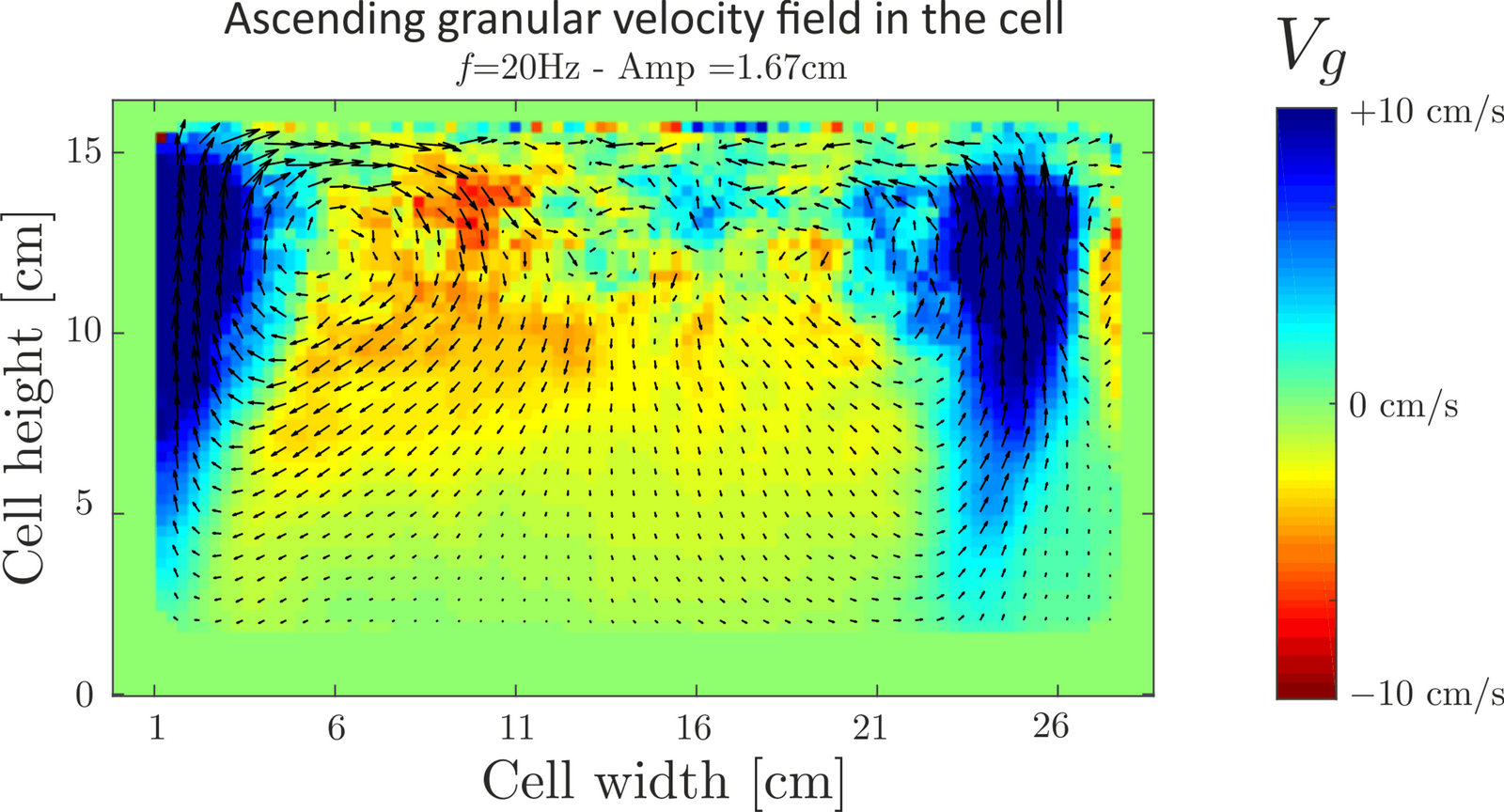
 Pour valider l'hypothèse de convection, le mouvement granulaire a été étudié grâce à une méthode PIV (Particular Image Velocimetry) qui calcule la vitesse des particules du milieu granulaire en tout point de la cellule à chaque image par cross correlation. Sur l'image ci-dessous, les branches ascendantes sont visibles en bleu sur les côtés de la cellule.
Pour valider l'hypothèse de convection, le mouvement granulaire a été étudié grâce à une méthode PIV (Particular Image Velocimetry) qui calcule la vitesse des particules du milieu granulaire en tout point de la cellule à chaque image par cross correlation. Sur l'image ci-dessous, les branches ascendantes sont visibles en bleu sur les côtés de la cellule.
Pour proposer une modélisation, nous avons défini deux forces qui peuvent s'appliquer sur l'objet :
 La force de flottabilité effective est l'équivalent d'une poussée d'Archimède pour le milieu granulaire. La masse volumique, le rayon, la vitesse du granulaire et le facteur géométrique sont donc des constantes dépendant du problème. La gravité est considérée comme compensée par le milieu granulaire et on retrouve en écrivant l'équilibre une équation différentielle dont la solution peut être déterminée :
La force de flottabilité effective est l'équivalent d'une poussée d'Archimède pour le milieu granulaire. La masse volumique, le rayon, la vitesse du granulaire et le facteur géométrique sont donc des constantes dépendant du problème. La gravité est considérée comme compensée par le milieu granulaire et on retrouve en écrivant l'équilibre une équation différentielle dont la solution peut être déterminée :
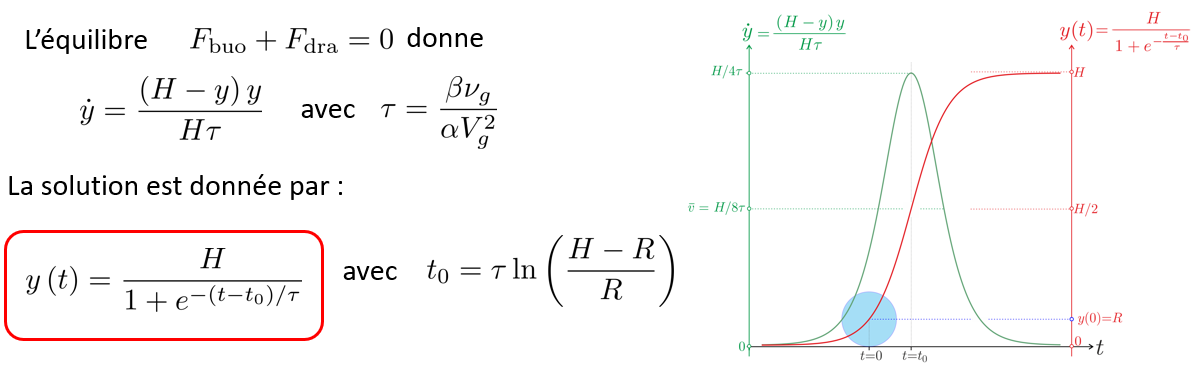
Nous avons considéré une vitesse moyenne de remontée égale à H/8τ pour définir un temps de remontée tel que :
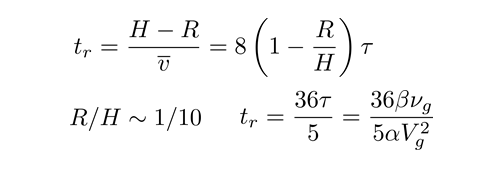
Les courbes expérimentales peuvent être retrouvée en superposant deux courbes de paramètres Vg différents.
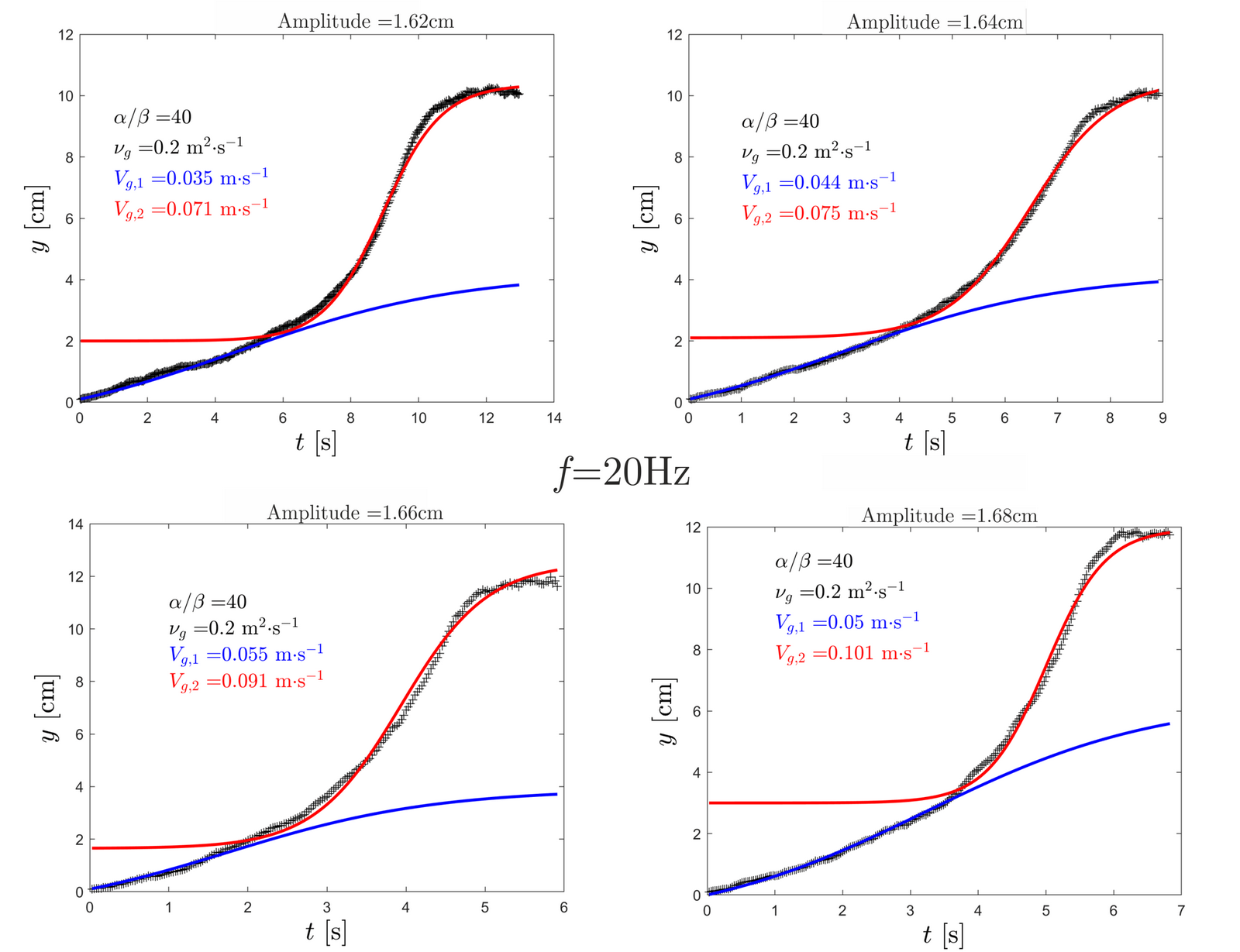
L'expérience a été reproduite pour différentes fréquences et amplitudes afin de trouver la méthode la plus efficace et de répondre au problème initial. Nous avons tracé la vitesse de remontée moyenne pour 20 Hz et 35 Hz pour étudier l'influence de la fréquence sur la remontée. Pour 20 Hz, la vitesse est plus élevée pour des faibles amplitudes comme on peut le voir sur le graphique ci-dessous. A haute fréquence, il faut augmenter fortement l'amplitude pour obtenir une vitesse de remontée égale à celle trouvée à 20 Hz.
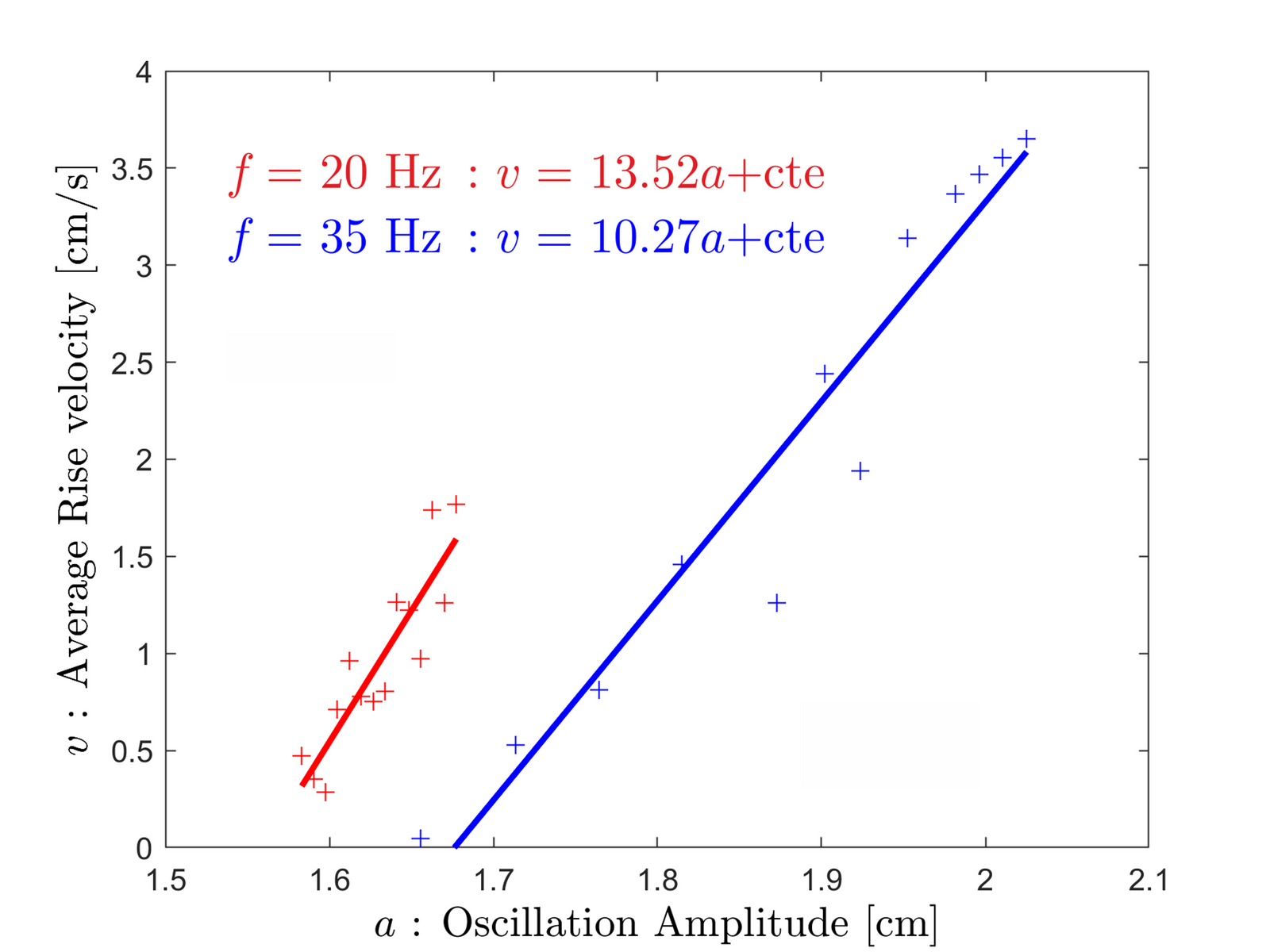 En se plaçant maintenant à la fréquence de 20 Hz, on trace la vitesse du milieu granulaire en faisant varier l'amplitude.
En se plaçant maintenant à la fréquence de 20 Hz, on trace la vitesse du milieu granulaire en faisant varier l'amplitude.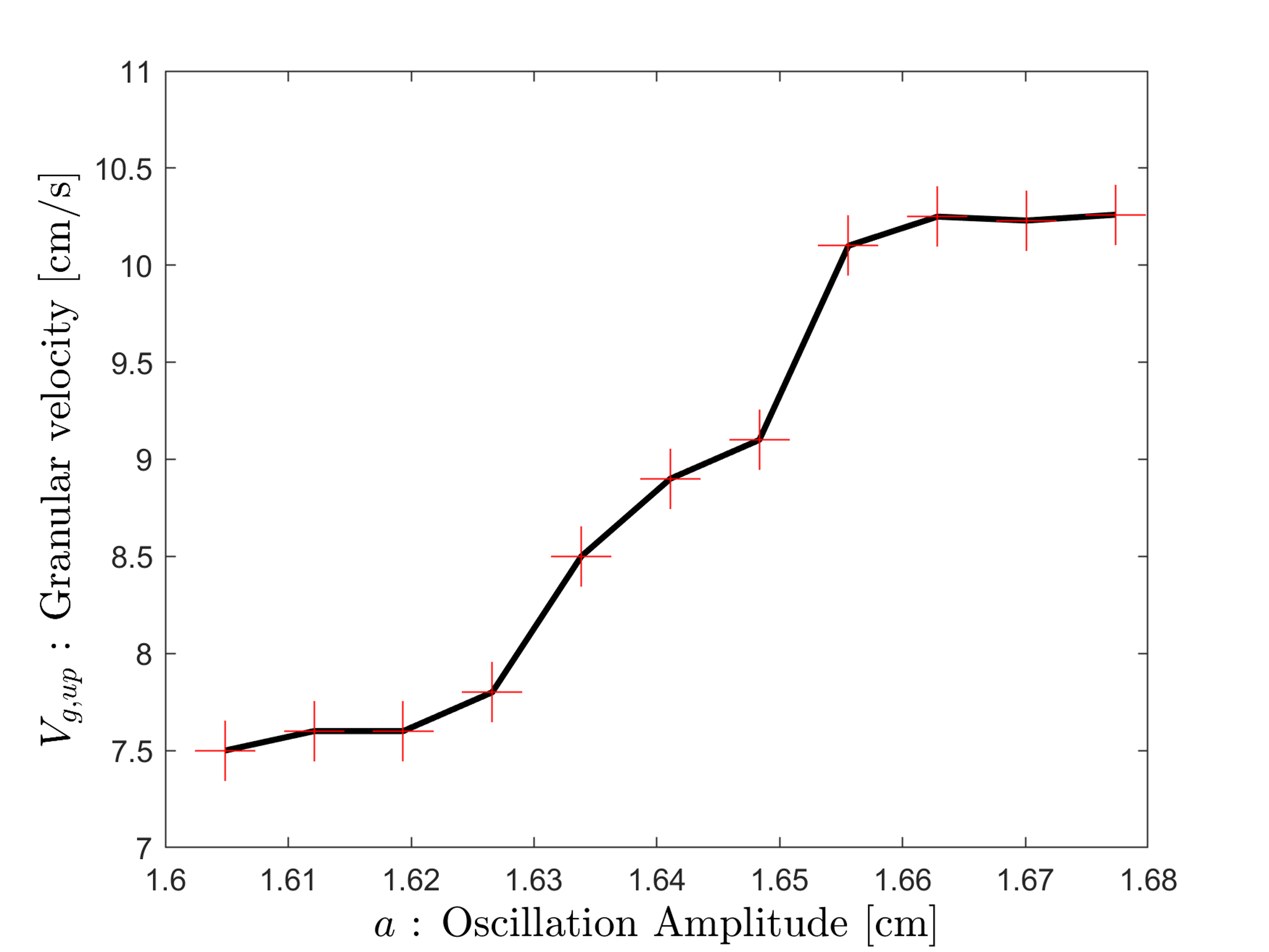 On observe une saturation de la vitesse du milieu granulaire et on en déduit le temps de remontée optimal que l'on peut espérer obtenir. On obtient un temps de remontée de 3.5 secondes. qui correspond aux résultats expérimentaux. En effet, pour une fréquence de 20 Hz et une amplitude de 1.68 cm, le temps de remontée était environ égal à 4 secondes.
On observe une saturation de la vitesse du milieu granulaire et on en déduit le temps de remontée optimal que l'on peut espérer obtenir. On obtient un temps de remontée de 3.5 secondes. qui correspond aux résultats expérimentaux. En effet, pour une fréquence de 20 Hz et une amplitude de 1.68 cm, le temps de remontée était environ égal à 4 secondes.
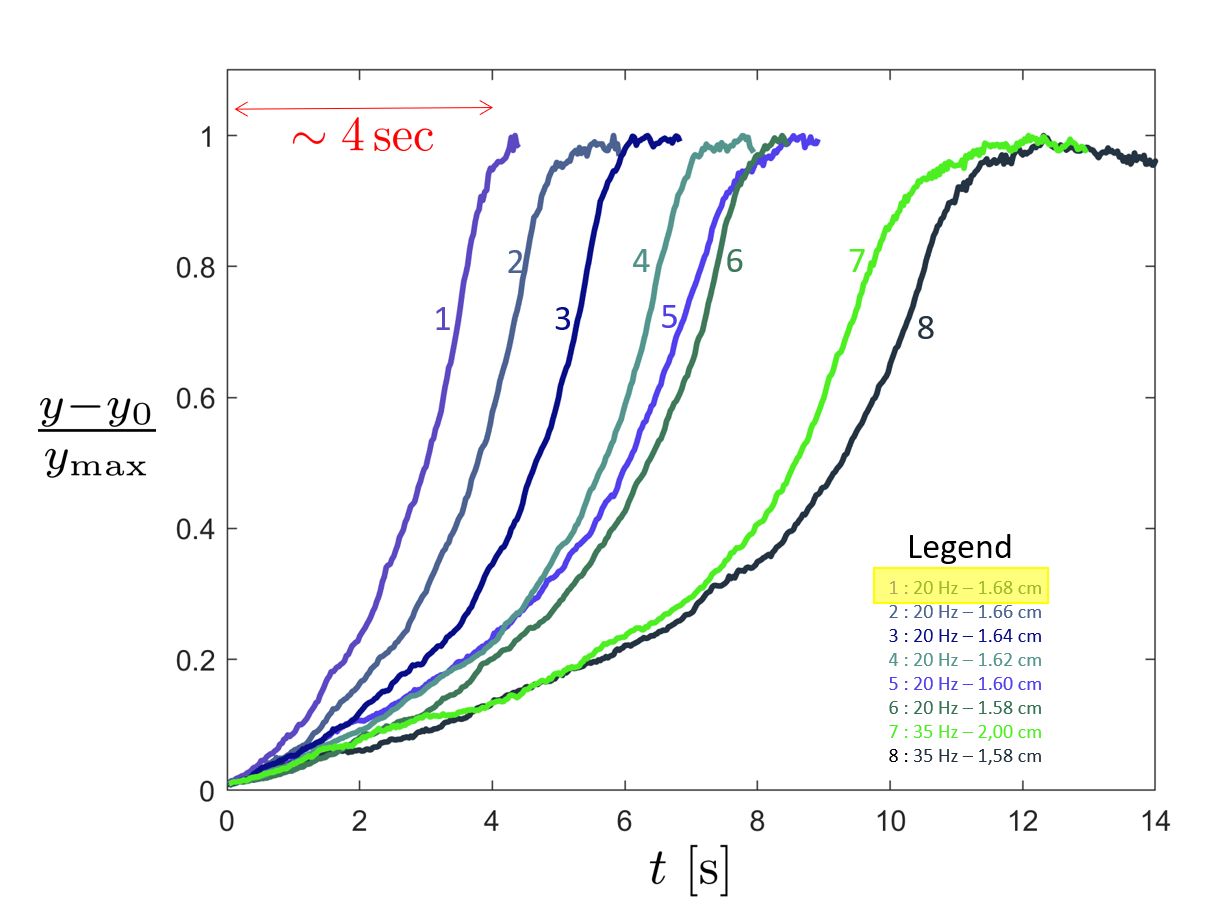 Ainsi, la vitesse de remontée augmente avec l'amplitude et a priori inversement de la fréquence, Une gamme de fréquences plus faibles pourrait donc être étudiée pour déterminer éventuellement une fréquence optimale.
Ainsi, la vitesse de remontée augmente avec l'amplitude et a priori inversement de la fréquence, Une gamme de fréquences plus faibles pourrait donc être étudiée pour déterminer éventuellement une fréquence optimale.
created with
Website Builder Software .