Galileo Method
Sujet #15:
Quelle est la hauteur maximale de laquelle un morceau de craie peut tomber sans se casser pour une surface donnée ?
De quels paramètres dépend cette hauteur ?
Existe-t-il des techniques de largage ou de lancement qui minimisent la probabilité de rupture ?
Montage de l’expérience principale


Pour obtenir une expérience reproductible, nous avons choisi d’utiliser une ficelle collée avec un point de colle en haut de la craie qui était ensuite lâchée.
Cette technique permettait également de contrôler la verticalité de la craie au moment du largage.
Premiers résultats
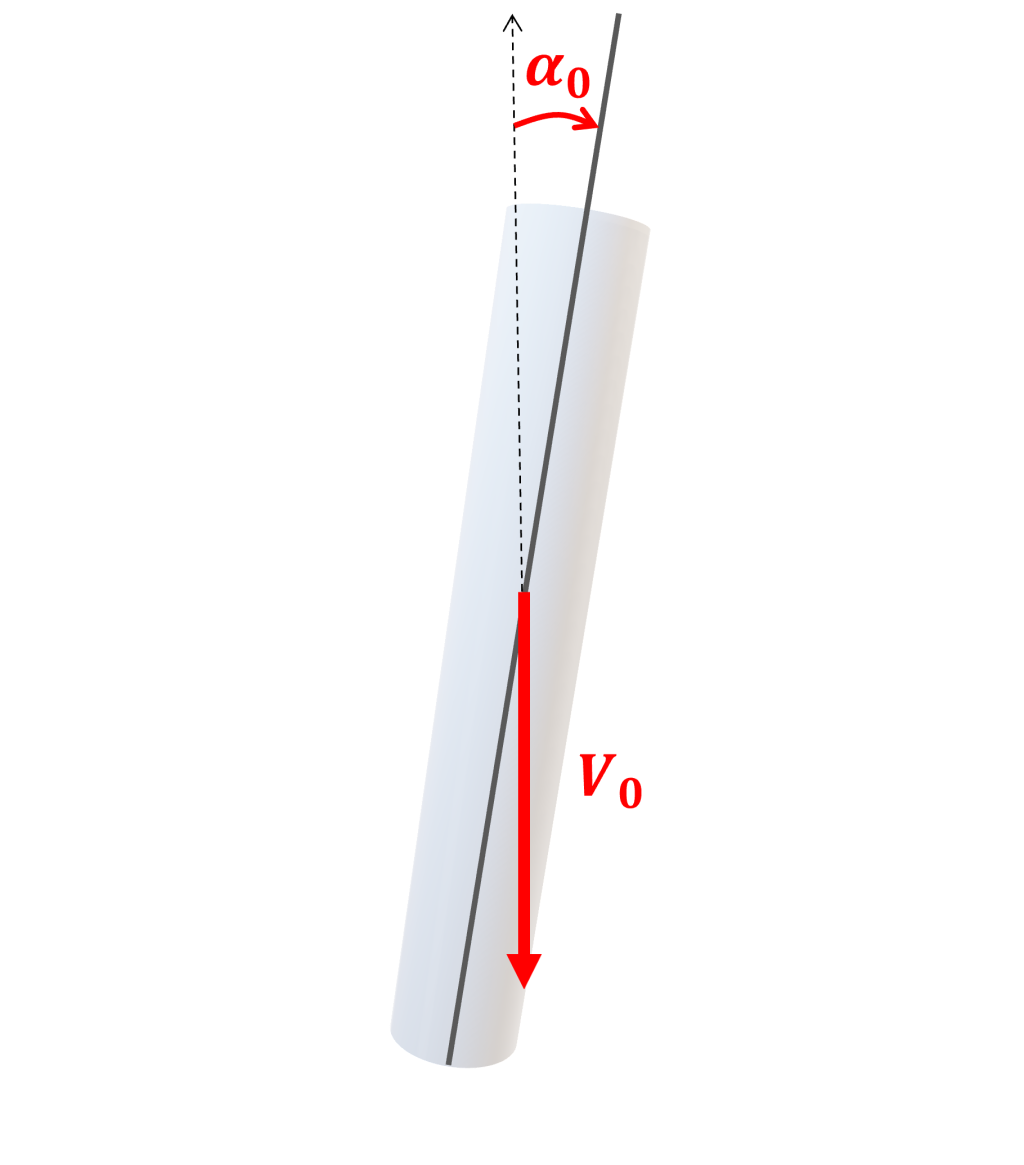
Nous avons effectué un grand nombre de lancers depuis une hauteur de 1m en faisant varier l’angle de chute et nous observons que pour des vitesses initiales nulles, la manière optimale de lâcher la craie est à la verticale. Dès que l’on donne de la vitesse à la craie, la probabilité de rupture à 1m devient non-nulle.
Etude du phénomène de rupture
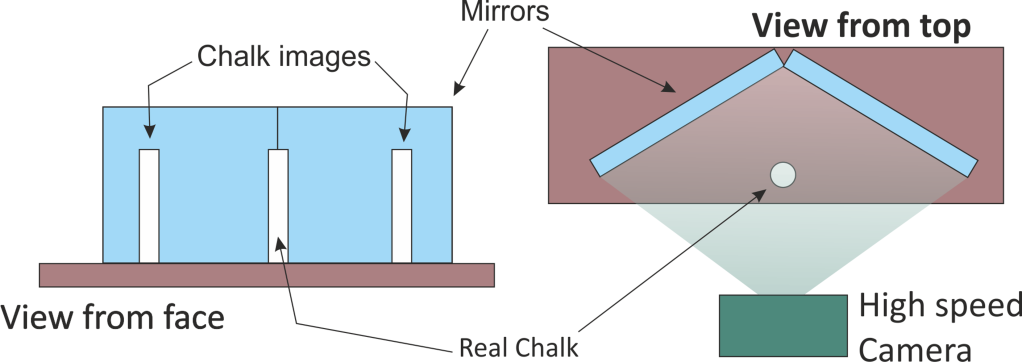
On filme le choc lors de l’arrivée de la craie sur le support avec une caméra ultra-rapide. Derrière la craie se trouvent deux miroirs qui permettent d’obtenir une vue à 360° de l’impact.

Paramètres d’étude
Surface d’atterrissage :

- Planche de bois : fine, légère (~0,2 kg), peu rigide
- Bloc de métal: épais, lourd (~14 kg), très rigide

Longueur de la craie : De 20 à 80mm
Défauts internes de la craie : Module de Young, fragilité initiale, porosité…
Influence des paramètres initiaux
Surface d’atterrissage :
- Planche en bois : La hauteur maximale de non-rupture mesurée est de 2,70m.
- Bloc de métal : La hauteur maximale de non-rupture mesurée est de 1,37m.

Cet écart s’explique par la différence de rigidité entre les deux supports. La planche en bois se courbe lors du choc (cf. image ci-contre) et en absorbe une partie de l’énergie alors que le bloc de métal demeure rigide et renvoie une onde de choc bien plus puissante dans la craie.
Longueur de la craie :
Pour des longueurs allant de 8cm (craie scolaire classique) à 2cm, nous avons largué des craies depuis différentes hauteurs puis nous avons répertorié leurs états à l’arrivée dans le graphique ci-dessous.
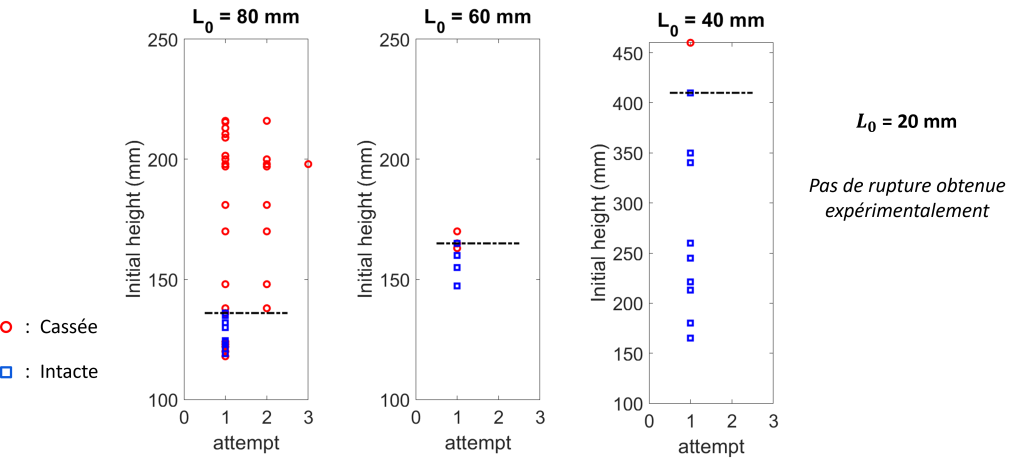
On notera bien que les tirets noirs font la séparation entre la zone depuis laquelle on peut lancer des craies et espérer les retrouver intactes et celle où elles se cassent systématiquement. Ils délimitent ainsi une hauteur maximale de non-rupture.
Comme on aurait pu s’y attendre intuitivement, cette hauteur maximale de non rupture croit décroit avec la longueur de la craie. De plus, on n’en a pas relevée pour des craies de 2cm.
Autres observations :
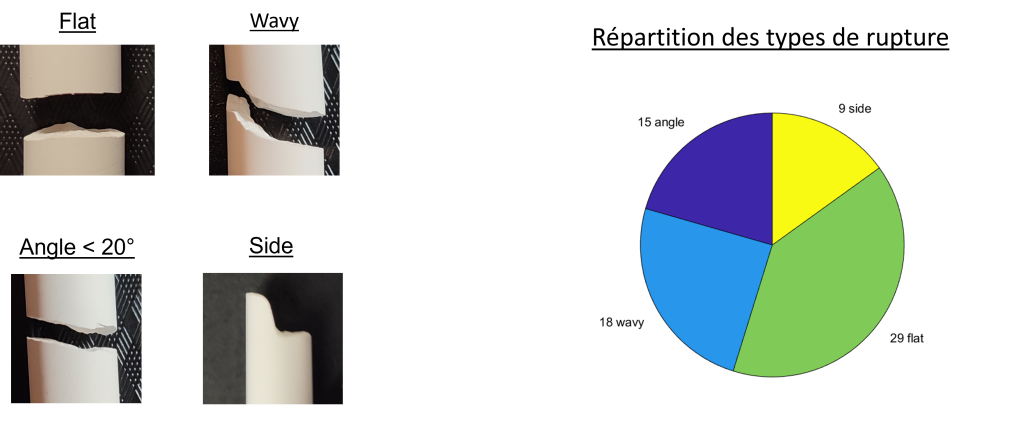
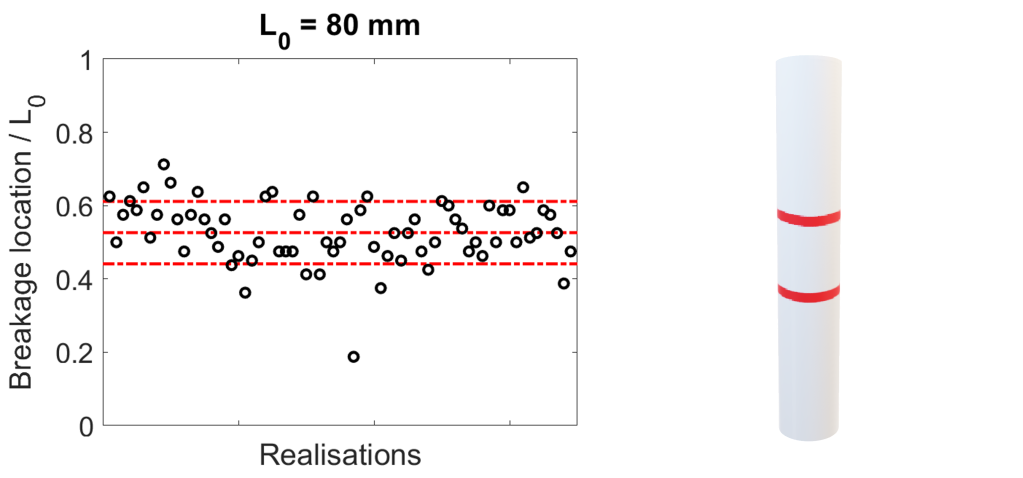
On remarque que la craie se rompt majoritairement entre 40% et 60% de sa longueur et que la rupture est nette et plate la plupart du temps.
Analyse et Modélisations
On s’intéresse à différentes modélisations pour essayer de comprendre comment la craie se brise mécaniquement et afin d’en apprendre plus sur les paramètres pertinents.
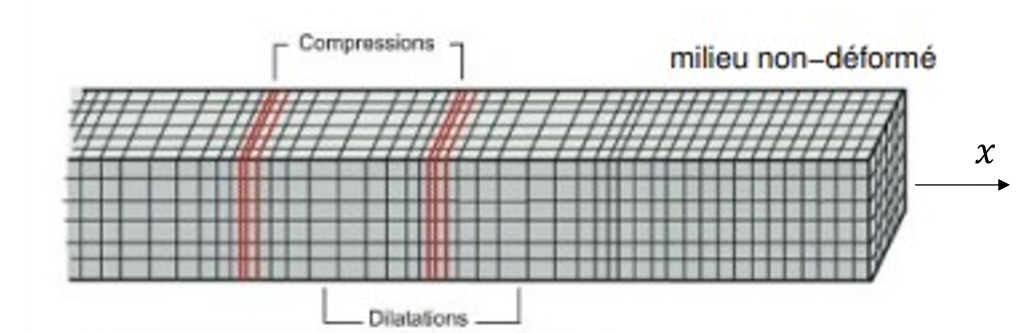
On considère un premier modèle de poutre dans laquelle une onde de traction-compression se propage d’équation :
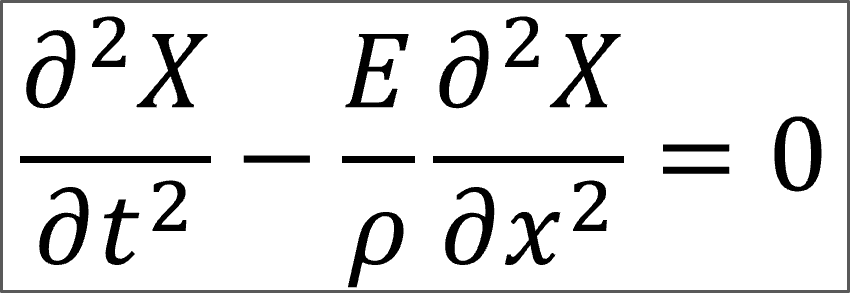
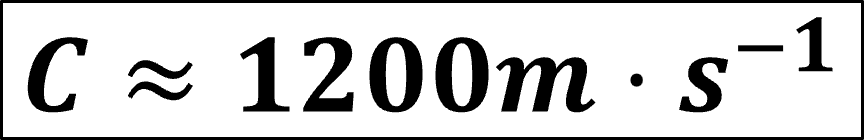
On obtient une vitesse :
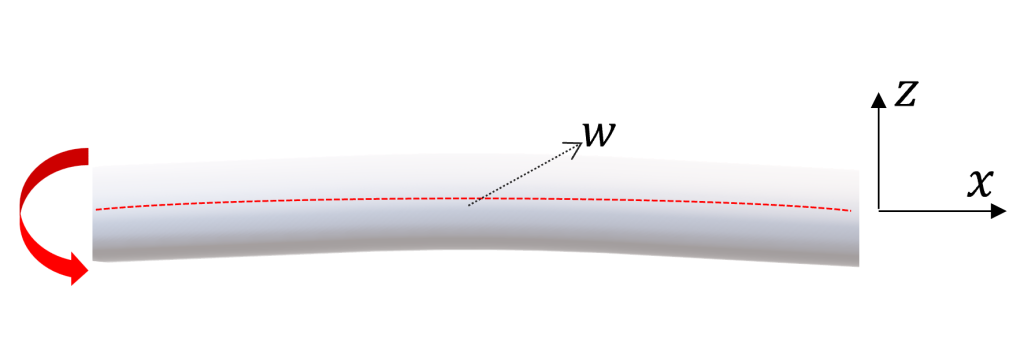
On considère un second modèle de flexion paramétré ci-dessus et d’équation :
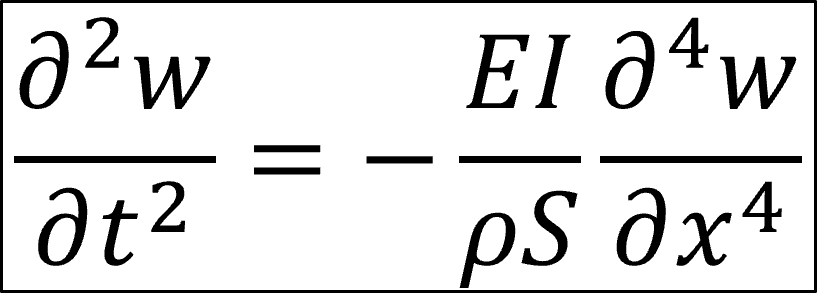

On obtient une vitesse :
Ces vitesses nous permettent de dire qu’on ne pourra pas déterminer quel phénomène est en jeu simplement grâce aux vidéos car il nous faudrait un nombre d’images par seconde bien supérieur à celui des caméras dont nous disposons.
On émet différentes hypothèses sur les causes de rupture :

Un train d’onde est émis au point de contact au sol, remonte la craie, se reflète en haut puis rencontre un autre train d’onde ce qui cause la rupture.

Le point de rupture correspond au point de flexion maximale.
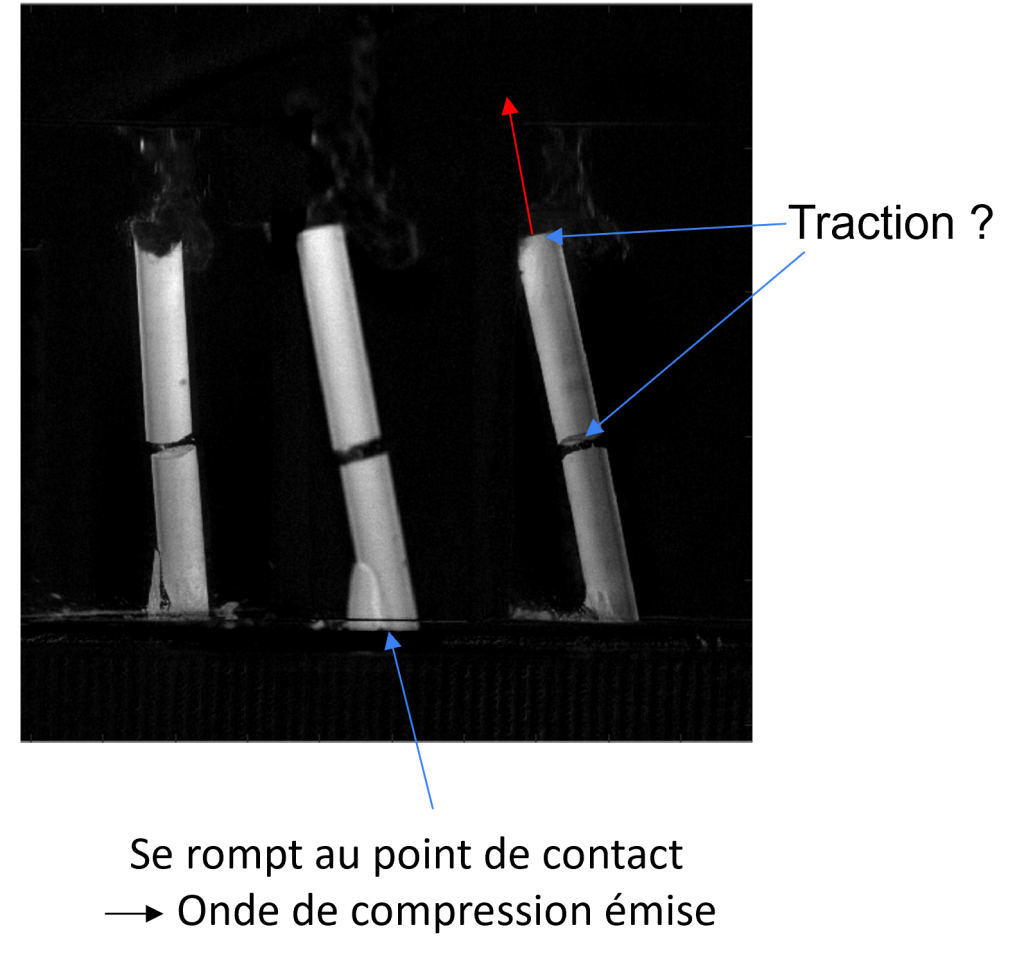
L’onde qui se propage depuis le sol tire sur la craie une fois arrivée en haut et provoque la rupture par traction.
On fait des expériences de traction et de compression pour regarder la manière dont les craies se brisent afin de déduire quelle était la bonne hypothèse.

Cette brisure correspond à ce que l’on obtient lors des largages de craies.

Cette brisure ne correspond pas vraiment à ce que l’on obtient expérimentalement.
Grâce aux essais de compression on peut tracer les courbes suivantes :
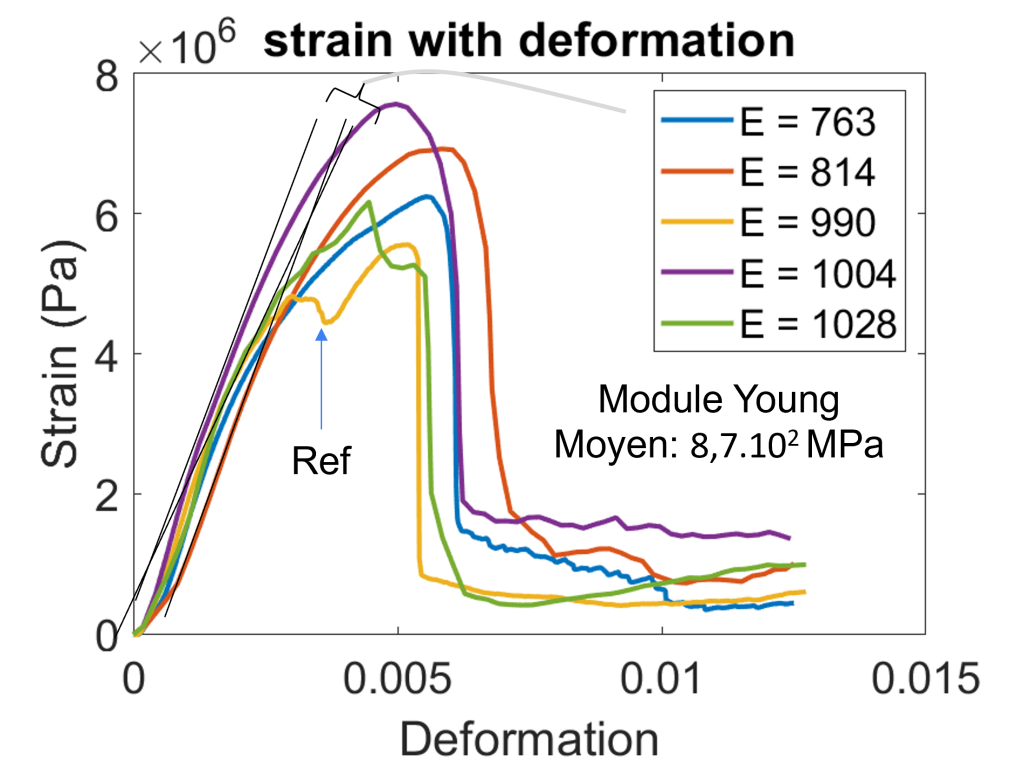
Le module d’Young ne renseigne pas quant à ce qu’il va se passer pour la craie : en effet, la courbe « Ref » a un module d’Young moyen par rapport aux autres et se rompt nettement plus tôt quand même.
On élimine donc l’hypothèse de compression.
Pour trancher entre les hypothèses de traction et de flexion, on effectue manuellement des essais de flexion :

Comme pour la traction, on obtient une fracture droite semblable à ce qui est observé lors des largages de craies.
Pour choisir la bonne hypothèse, on taille les craies en pointes ce qui permet d’avoir moins de flexion à l’atterrissage.

On observe alors des hauteurs maximales de non-rupture plus élevées que pour les craies dont l’extrémité est laissée plate.
On en déduit que le phénomène dominant mis en jeu est celui de flexion.
Cette étude nous permet également d’expliquer les différents profils de ruptures des craies :

En résumé…
- La hauteur maximale est entre 1,37m (pour l’acier) et 2,70 m (pour le bois épais).
- Elle dépend de la longueur et de la fragilité intérieure du bâton de craie.
- La flexion est le phénomène majeur.
- La chute verticale semble être la technique optimale.
L’affûtage de la pointe est une solution.

