stephanie.chaillat at ensta-paristech.fr

Stéphanie CHAILLAT-LOSEILLE         

Junior Scientist (CR2 CNRS)

Laboratoire POems

(UMR 7231 CNRS-INRIA-ENSTA)




ENSTA-UMA

828, Bd des Maréchaux

91 762 Palaiseau Cedex, FRANCE

Office 2226

Phone: +33 (0)1 81 87 20 83

PAPERS


2. S. C., M. Bonnet, Recent advances on the Fast Multipole Accelerated Boundary Element Method for 3-D elastodynamics, Special Issue Modelling of Waves in Solids, Wave Motion, Vol. 50, 1090-1104,2013. [Preprint] [Pdf]

 


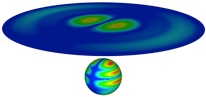
  1. 1. S. C., M. Bonnet, A new Fast Multipole formulation for the Elastodynamic Half-Space Green’s tensor, Journal of Computational Physics, Vol. 258, 787-808, 2014.[Preprint] [Pdf]

In this article, a version of the frequency-domain elastodynamic Fast Multipole-Boundary Element Method (FM-BEM) for semi-infinite media, based on the half-space Green's tensor (and hence avoiding any discretization of the planar traction-free surface), is presented. The half-space Green's tensor is often used (in non-multipole form until now) for computing elastic wave propagation in the context of soil-structure interaction, with applications to seismology or civil engineering. However, unlike the full-space Green's tensor, the elastodynamic half-space Green's tensor cannot be expressed using derivatives of the Helmholtz fundamental solution. As a result, multipole expansions of that tensor cannot be obtained directly from known expansions, and are instead derived here by means of a partial Fourier transform with respect to the spatial coordinates parallel to the free surface. The obtained formulation critically requires an efficient quadrature for the Fourier integral, whose integrand is both singular and oscillatory. Under these conditions, classical Gaussian quadratures would perform poorly, fail or require a large number of points. Instead, a version custom-tailored for the present needs of a methodology proposed by Rokhlin and coauthors, which generates generalized Gaussian quadrature rules for specific types of integrals, has been implemented. The accuracy and efficiency of the proposed formulation is demonstrated through numerical experiments on single-layer elastodynamic potentials involving up to about N=6 105 degrees of freedom. In particular, a complexity significantly lower than that of the non-multipole version is shown to be achieved.http://www.sciencedirect.com/science/article/pii/S0021999113007602
 

This article is mainly devoted to a review on fast BEMs for elastodynamics, with particular attention on fast multipole methods (FMMs). It also includes original results that complete a very recent study on the FMM for elastodynamic problems in semi-infinite media. The main concepts underlying fast elastodynamic BEMs and the kernel-dependent elastodynamic FM-BEM based on the diagonal-form kernel decomposition are reviewed. An elastodynamic FM-BEM based on the half-space Green's tensor suitable for semi-infinite media, and in particular on the fast evaluation of the corresponding governing double-layer integral operator involved in the BIE formulation of wave scattering by underground cavities, is then presented. Results on numerical tests for the multipole evaluation of the half-space traction Green's tensor and the FMM treatment of a sample 3D problem involving wave scattering by an underground cavity demonstrate the accuracy of the proposed approach. The article concludes with a discussion of several topics open to further investigation, with relevant published work surveyed in the process.

 

This article extends previous work by the authors on the single- and multi-domain time-harmonic elastodynamic multi-level fast multipole BEM formulations to the case of weakly dissipative viscoelastic media. The underlying boundary integral equation and fast multipole formulations are formally identical to that of elastodynamics, except that the wavenumbers are complex-valued due to attenuation. Attention is focused on evaluating the multipole decomposition of the viscoelastodynamic fundamental solution. A damping-dependent modification of the selection rule for the multipole truncation parameter, required by the presence of complex wavenumbers, is proposed. It is empirically adjusted so as to maintain a constant accuracy over the damping range of interest in the approximation of the fundamental solution, and validated on numerical tests focusing on the evaluation of the latter. The proposed modification is then assessed on 3D single-region and multi-region visco-elastodynamic examples for which exact solutions are known. Finally, the multi-region formulation is applied to the problem of a wave propagating in a semi-infinite medium with a lossy semi-spherical inclusion (alluvial basin). These examples involve problem sizes of up to about 3 105 boundary unknowns.

5. S.C., J.F. Semblat, M. Bonnet, A preconditioned  3-D multi-region fast multipole solver for seismic wave propagation in complex geometries. Communications in Computational Physics (special issue WAVES 2009), Vol. 11, 594-609, 2012. [Preprint] [Pdf]

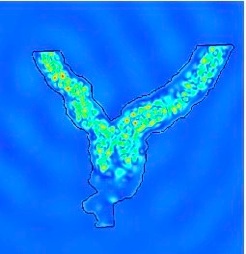
The analysis of seismic wave propagation and amplification in complex geological structures requires efficient numerical methods.  In this article, following up on recent studies devoted to the formulation, implementation and evaluation of 3-D single- and multi-region elastodynamic fast multipole boundary element methods (FM-BEMs), a simple preconditioning strategy is proposed. Its efficiency is demonstrated on both the single- and multi-region versions using benchmark examples (scattering of plane waves by canyons and basins). Finally, the preconditioned FM-BEM is applied to the scattering of plane seismic waves in an actual configuration (alpine basin of Grenoble, France), for which the high velocity contrast is seen to significantly affect the overall efficiency of the multi-region FM-BEM.

6. H.D. Bui, S. C., A. Constantinescu, E. Grasso, Identification of a planar crack in Zener type viscoelasticity, Annals of Solid and Structural Mechanics, Vol. 1, 3-8, 2010. [Pdf]


7. H.D. Bui, S. C., On a nonlinear inverse problem in viscoelasticity. Vietnam Journal of Mechanics, 31:211-219, 2009.


8. S.C., M. Bonnet, J.F. Semblat, A new fast multi-domain BEM to model seismic wave propagation and amplification in 3D geological structures, Geophys. J. Int. , Vol. 177, 509-531, 2009. [Preprint] [Pdf]

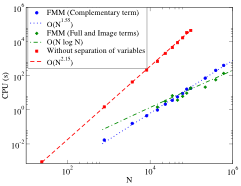
The analysis of seismic wave propagation and amplification in complex geological structures raises the need for efficient and accurate numerical methods. The solution of the elastodynamic equations using traditional boundary element methods (BEMs) is greatly hindered by the fully-populated nature of the matrix equations arising from the discretization. In a previous study limited to homogeneous media, the present authors have established that the Fast Multipole (FM) method reduces the complexity of a 3-D elastodynamic BEM  to $N \log N$ per GMRES iteration and demonstrated its effectiveness on 3-D canyon configurations. In this article, the frequency-domain FM-BEM methodology is extented to 3-D elastic wave propagation in piecewise-homogeneous domains in the form of a  FM-accelerated multi-region BE-BE coupling approach. This new method considerably enhances the capability of the BEM for studying   the propagation of seismic waves in 3-D alluvial basins of arbitrary geometry embedded in semi-infinite media. Several fully 3-D examples (oblique SV-waves) representative of such configurations validate and demonstrate the capabilities of the multi-domain fast multipole approach. They include comparisons with available (low-frequency) results for various types of incident wavefields, and time-domain results obtained by means of Fourier synthesis.

9. S.C., M. Bonnet, J.F. Semblat, A Fast Multipole accelerated BEM for 3-D elastic wave computation, Revue Europeenne de Mecanique Numerique, Vol. 17, 701-712, 2008. [Preprint] [Pdf]


10. S.C., M. Bonnet, J.F. Semblat, A multi-level fast multipole BEM for 3-D elastodynamics in the frequency domain, Computer Methods in Applied Mechanics and Engineering, Vol. 197, 4233-4249, 2008.[Preprint] [Pdf]  

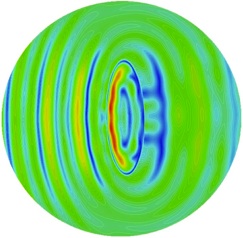
To reduce computational complexity and memory requirement for 3-D elastodynamics using the boundary element method (BEM), a multi-level fast multipole BEM (FM-BEM) is proposed. The diagonal form for the expansion of the elastodynamic fundamental solution is used, with a truncation parameter adjusted to the subdivision level, a feature necessary for achieving optimal computational efficiency. Both the single-level and multi-level forms of the elastodynamic FM-BEM are considered, with emphasis on the latter.  Crucial implementation issues, including the truncation of the multipole expansion, the optimal number of levels, the direct and inverse extrapolation steps are examined in detail with the backing of numerical experiments. A complexity analysis for both the single-level and multi-level versions is conducted. The correctness and computational performances of the proposed elastodynamic FMM are demonstrated on numerical examples featuring up to O(106) DOFs run on a single-processor PC.

11. S.C., H.D. Bui, Resolution of linear viscoelastic equations in the frequency domain using real Helmholtz boundary integral equations, C. R. Mecanique, Vol. 335, 746-750, 2007. [Preprint] [Pdf]


12. S. C., M. Bonnet, J.F. Semblat, A Fast Multipole Method formulation for 3D elastodynamics in the frequency domain, C. R. Mecanique, Vol. 335, 714-719, 2007. [Preprint] [Pdf]

PAPERS UNDER REVIEW OR IN PREPARATION


  1. 1. M. Bonnet, S. C., J.F. Semblat, Multi-level fast multipole BEM for 3-D elastodynamics, In Recent Advances in BEM (D. Polyzos and G. Manolis, eds.), 15-27, 2009. [Preprint] [Pdf]


  1. 1. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. University of Zurich, March 2014.

  2. 2. A new analytic preconditioner for the Fast Multipole Accelerated Boundary Element Method in 3-D elastodynamics. University of Parma, Italy, February 2014.


  1. 3. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire Equipe EDP LJK, Grenoble, November 2013.

  2. 4. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire Equipe SIN, MSSMAT, Centrale Paris, November 2013.

  3. 5. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire POEMS, Paris, February 2013.

  4. 6. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire ISTERRE, Grenoble, February 2013.

  5. 7. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire du LMA, Marseille, France, January 2013.


  1. 8. Fast multipole accelerated boundary integral equation method for 3-D elastodynamic problems in a half-space. Séminaire du LaMSID, EDF R&D Clamart,  France,  September 2012.


  1. 9. Fast Multipole Method for 3-D elastodynamic and viscoelastodynamic boundary integral equations. Séminaire de l'équipe Analyse Numérique de l’IRMAR, Université Rennes 1,  France,  June 2011.

  2. 10. Fast Multipole Method for 3-D elastodynamic and viscoelastodynamic boundary integral equations. Seminar of the Department of Mathematics, Parma University,  Italy, June 2011.

  3. 11. FaIMS : Un algorithme rapide pour un problème inverse en diffraction acoustique. Séminaire de l'équipe projet DEFI, INRIA Saclay,  France,  March 2011.


  1. 12. Forward and inverse fast numerical methods for wave propagation. Séminaire de l'équipe projet POems, INRIA Rocquencourt,  France,  December 2009.

  2. 13. Forward and inverse fast numerical methods for wave propagation. LMS, Ecole Polytechnique,  France,  November 2009.

  3. 14. Forward and inverse fast numerical methods for wave propagation. ENAC, Ecole Polytechnique Federale de Lausanne, Switzerland, October 2009.

  4. 15. Fast Multipole Method for 3-D elastodynamic boundary integral equations. Application to multi-region elastic wave propagation problems. CSELA, Georgia Institute of Technology, USA, Febrary 2009.


  1. 16. Fast Multipole Method for 3-D elastodynamic boundary integral equations. Application to multi-region elastic wave propagation problems. Seminar of the institute of applied mechanics, Graz University of Technology, Austria, November 2008.


  1. 17. Presentation of the Fast Multipole Method formulation for 3D elastodynamics in the frequency domain, QSHA meeting, LCPC Paris, France, November 2006.

  2. 18. Fast Multipole Method formulation for 3D elastodynamics in the frequency domain: single-level algorithm, LCPC seminar, LCPC Paris, France, January 2006.

BOOK CHAPTER

  1. 1. S. C., Fast Multipole Method for 3-D elastodynamic boundary integral equations. Application to seismic wave propagation, ENPC, 2008. [Dissertation-pdf] [Presentation-Pdf]

PhD DISSERTATION
CONFERENCES

  1. 1. S.C., M. Darbas, F. Le Louër, A new analytic preconditioner for the iterative solution of Dirichlet exterior scattering problems in 3D elasticity, WCCM, Barcelona, Spain, July 2014


  1. 2. S.C.*, G. Biros, A fast and Adaptive Algorithm for the inverse medium problem based on Singular Values Decomposition, 3rd European Conference on Computational Optimization, Chemnitz, Germany, July 2013.

  2. 3. S.C.*, A. Loseille, An Adapted Fast Multipole Accelerated Boundary Element Method for 3D Elastodynamics, SIAM in the Geosciences, Padua, Italy, June 2013.

  3. 4. J. Virieux, R. Brossier, S.C., A. Duchkov, E. Etienne, B. Lombard, S. Operto, A. Serdyukov, Seismic Elastic Modeling for Seismic Imaging, SIAM in the Geosciences, Padua, Italy, June 2013.

  4. 5. S.C., M. Bonnet, Fast Multipole Accelerated Boundary Element Method for problems in an elastic Half-Space, WAVES, Tunis, Tunisia, June 2013.

  5. 6.S.C.*, M. Bonnet, Comparison of two Fast Multipole Accelerated Boundary Element Methods for 3D elastodynamic problems in a semi-infinite media, IABEM2013, Santiago, Chile, January 2013.


  1. 7. S.C.*, M. Bonnet, A New Fast Multipole Method for 3D Elastodynamics based using the Half-Space Fundamental Solutions, EUROMECH Colloquium 540: Advanced Modelling of Wave Propagation in Solids, Prague, Czech Republic, October 2012.

  2. 8. S.C.*, M. Bonnet, A New Fast Multipole Method for Elasticity based on the Half-Space Fundamental Solutions, 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, September 2012.

  3. 9. S.C.*, M. Bonnet, Formulation and Fast Evaluation of the Multipole Expansions of the Elastic Half-Space  Fundamental Solutions, 8th European Solid Mechanics Conference, Graz, Austria, July 2012.

  4. 10. E. Grasso, S. C., M. Bonnet,  J.F. Semblat, Coupling the Finite Element Method and the Fast Multipole Boundary Element Method in 3-D Viscoelastodynamics, 8th European Solid Mechanics Conference, Graz, Austria, July 2012.

  5. 11. S.C.*, M. Bonnet, A new fast  multipole formulation for the elastodynamic half-space  fundamental solutions, 4th Workshop BEM on the Saar, Saarbrücken, Germany, May 2012.


  1. 12. S. C.*, G. Biros, A fast and adaptive algorithm for the inverse medium problem with multiple frequencies and multiple sources for the 3-D elastodynamic equation, 8th International Conference on Structural Dynamics (Eurodyn 2011), Leuven, Belgium, July 2011.

  2. 13. S. C.*, G. Biros, Algorithme rapide et adaptatif pour le problème inverse de milieu pour l’équation des ondes scalaire avec fréquences et sources multiples, 10eme Colloque National en Calcul des Structures, Giens, May 2011. [Preprint]

  3. 14. E. Grasso, S. C., J.F. Semblat, M. Bonnet, Méthode multipôle rapide multi-niveaux en visco-élastodynamique 3-D, 10eme Colloque National en Calcul des Structures, Giens, May 2011. [Preprint]

  4. 15. S. C., G. Biros, A Fast Algorithm for the Time Harmonic Elastic Inverse Medium with Multiple Events, SIAM CSE, Reno, USA, March 2011.


  1. 16. S. C.*, G. Biros, General fast inversion method to recover small 3-D inhomogeneities using a small number of sources and excitation frequencies, IV European Congress on Computational Mechanics  (ECCM 2010), Paris, France, May 2010.

  2. 17. E. Grasso, R. Bost, S. C., J.F. Semblat, M. Bonnet, Multi-level fast multipole BEM for the complex-wavenumber formulation of 3-D viscoelastodynamics, IV European Congress on Computational Mechanics (ECCM 2010), Paris, France, May 2010.

  3. 18. S. C., H.D. Bui, On the identification of an inhomogeneity in viscoelasticity, IV European Congress on Computational Mechanics  (ECCM 2010), Paris, France, May 2010.

  4. 19. A. Constantinescu, H.D. Bui, S. C., E. Grasso, Identification of a planar crack in Zener type viscoelasticity, IV European Congress on Computational Mechanics  (ECCM 2010), Paris, France, May 2010.

  5. 20. S. C.*, G. Biros, FaIMS: A Fast Algorithm for the Inverse Medium Problem in Acoustic Scattering, SIAM Conference on Imaging Science, Chicago, USA, April 2010. [Pdf presentation]


  1. 21. S. C.*, M. Bonnet, J.F. Semblat, Fast multipole method for 3D elastodynamic boundary integral equations. Application to seismic wave propagation, COMPDYN 2009, Rhodes, June 2009 (Invited talk).

  2. 22. S. C., M. Bonnet, J.F. Semblat, A new fast BEM for 3-D multi-domain elastic wave propagation problems, WAVES 2009, Pau, June 2009.

  3. 23. S. C.*, M. Bonnet, J.F. Semblat, Fast multipole method for 3D elastodynamic boundary integral equations. Application to seismic wave propagation, 9eme Colloque National en Calcul des Structures, Giens, May 2009 (Plenary talk).

  4. 24. S. C., M. Bonnet, J.F. Semblat, Fast multipole accelerated boundary element method for elastic wave propagation in multi-region domains, 9eme Colloque National en Calcul des Structures, Giens, May 2009.


  1. 25. S. C., M. Bonnet, J.F. Semblat, Diffraction of seismic waves from 3-D canyons and alluvial basins modeled using the fast multipole accelerated BEM, 14 WCEE, Beijing, October 2008.

  2. 26. S. C.*, M. Bonnet, J.F. Semblat, A multi-level fast multipole multi-region method for 3D seismic response of alluvial basins, WCCM8, Venice, July 2008. 

  3. 27. S. C., J.F. Semblat, M. Bonnet, A multi-level fast multipole multi-region method for 3-D frequency-domain elastodynamics, EM08, Minneapolis, May 2008.

  4. 28. S. C., J.F. Semblat, M. Bonnet, A multi-level fast multipole multi-region method for 3-D elastodynamics in the frequency domain, GAMM2008, Bremen, April 2008.


  1. 29. S. C.*, M. Bonnet, J.F. Semblat, Diffraction of seismic wave from 3-D canyons and alluvial basins modeled using the Fast Multipole-accelerated BEM, American Geophysical Union fall meeting, San Francisco, December 2007. 

  2. 30. S. C.*, M. Bonnet, J.F. Semblat, Accélération des calculs de propagation d'ondes elastiques par la Methode multipole rapide (formulation par equations integrales de frontiere), 18eme Congres Français de mecanique, Grenoble, August 2007.

  3. 31. S. C.*, M. Bonnet, J.F. Semblat, Fast multipole boundary integral equation method for 3D seismic wave propagation in alluvial basins, 9th US National Congress on Computational Mechanics, San Francisco, July 2007. 

  4. 32. S. C.*, M. Bonnet, J.F. Semblat, Modélisation de la propagation d'ondes sismiques en 3D par la "Methode multipole rapide" , 7eme Colloque National AFPS 2007, Paris, July 2007.

  5. 33. S. C.*, M. Bonnet, J.F. Semblat, A new fast BEM method to model site effects in alluvial basins, 4th International Conference on Earthquake Geotechnical Engineering, Thessalonique, June 2007.

  6. 34. S. C., M. Bonnet, J.F. Semblat, A fast multipole accelerated BEM for 3-D seismic wave computation, Computational Methods in Structural Dynamics and Earthquake Engineering, Rethymno, June 2007.

  7. 35. S. C.*, M. Bonnet, J.F. Semblat, Methode multipole rapide pour les elements de frontiere en elastodynamique tridimensionnelle : application a la propagation d'ondes sismiques, 8eme Colloque National en Calcul des Structures, Giens, France, May 2007.

  8. 36. S. C.*, M. Bonnet, J.F. Semblat, Fast Multipole Method formulation for 3D elastodynamics in the frequency domain, 23rd Annual GAMM-Seminar Leipzig on Integral Equation Methods for High-frequency Scattering Problems, Leipzig, January 2007.

SEMINARS


4. S. C., G. Biros, An adaptive algorithm for the inverse medium problem with multiple frequencies and multiple sources for the scalar Helmholtz equation, in preparation.

4. E. Grasso, S. C., M. Bonnet, J.F. Semblat, Application of the multi-level time-harmonic fast multipole BEM to 3-D visco-elastodynamics, Engineering Analysis with Boundary Elements, Vol. 36, 744-758, 2012. [Preprint] [Pdf]

We consider the inverse medium problem for the time-harmonic wave equation with broadband and multi-point illumination in the low frequency regime. Such a problem finds many applications in geosciences (e.g. ground penetrating radar), non-destructive evaluation (acoustics), and medicine (optical tomography).  We use an integral-equation (Lippmann-Schwinger) formulation, which we discretize using a quadrature method. We consider only small perturbations of the background medium(Born approximation). To solve this inverse problem, we use a least squares formulation that is regularized with the truncated Singular Value Decomposition (SVD). If Nfr is the number of excitation frequencies, Ns the number of incoming waves, Nd the number of detectors, and N the parameterization for the scatterer, a dense singular value decomposition for the overall input-output map will have [min(Ns Nfr Nd, N)]2 x max(Ns Nfr Nd, N) cost. We have developed a fast SVD approach that brings the cost down to O( N Nfr Nd +N Nfr Ns) thus, providing orders of magnitude improvements over a black-box dense SVD.  We provide numerical results that demonstrate the scalability of the method.

3. S. C., G. Biros, FaIMS: A fast algorithm for the inverse medium problem with multiple frequencies and multiple sources for the scalar Helmholtz equation, Journal of Computational Physics, Vol. 231, 4403-4421, 2012. [Preprint] [Pdf]


1. S. C., M. Darbas, F. Le Louër, An on-surface radiation conditions for 3D time-harmonic elastic scattering problems: the Dirichlet boundary condition case, under review.

In this paper, we investigate a fast and approximate method, called the On-Surface Radiation Condition (OSRC) method, for solving scattering problems of time-harmonic elastic waves by a three-dimensional rigid obstacle. The proposed OSRC is given by a local and accurate enough approximation of the Modified Dirichlet-to-Neumann map (DtN). Our main contribution is to propose a methodology to evaluate the DtN in a fast way. A detailed numerical study is presented to optimize the different parameters of the method. The efficiency and accuracy of the approach are demonstrated on various obstacle geometries at high frequencies.


  1. 2.S. C., F. Collino, A Stable Multiscale Fast Multipole Method for the Helmholtz Kernel : Theoretical Developments, under review.

This work presents a  proposition for a new Fast Multipole Method based on plane wave expansions combining the advantages of low and high frequency formulations. We revisit  the method of Greengard et al. devoted to the low frequency regime and based on breaking down  Green's function into a propagative part and an evanescent one. More precisely, we  give an explicit formula  of the filtered translation function for the propagative part,  derive a new formula for the evanescent part   and   provide a new interpolation algorithm. At all stages, we check the accuracy of the method by providing error estimates. Using these new tools, we construct a combined algorithm. The stability and accuracy of this new method is illustrated in an example which is known to be difficult for traditional FMM.


3. K. Meza-Fajardo, J.F. Semblat, S. C., Seismic Wave Amplification in 3D Alluvial Basins: Fast Multipole accelerated BEM based simulations and aggravation factors, in preparation.